题目内容
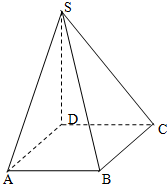
如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.
(1)求证:CD⊥AE;
(2)求证:AE⊥平面PCD;
(3)求直线AC与平面PCD所成的角的大小的正弦..

(1)求证:CD⊥AE;
(2)求证:AE⊥平面PCD;
(3)求直线AC与平面PCD所成的角的大小的正弦..

(1)取AD的中点O,由正△PAD可得PO⊥AD,
∵平面PAD⊥平面ABCD,∴PO⊥平面ABCD,∴PO⊥CD.
又∵CD⊥AD,PO∩AD=O,
∴CD⊥平面PAD,
∴CD⊥AE.
(2)由(1)可知:CD⊥AE.
∵E为正三角形PAD的边PD的中点,∴AE⊥PD.
∵CD∩PD=D,∴AE⊥平面PCD.
(3)由(2)可知:AE⊥平面PCD.
∴∠ACE即为直线AC与平面PCD所成的角.
不妨设AD=2.
则AE=
,AC=2
.
∴sin∠ACE=
=
.

∵平面PAD⊥平面ABCD,∴PO⊥平面ABCD,∴PO⊥CD.
又∵CD⊥AD,PO∩AD=O,
∴CD⊥平面PAD,
∴CD⊥AE.
(2)由(1)可知:CD⊥AE.
∵E为正三角形PAD的边PD的中点,∴AE⊥PD.
∵CD∩PD=D,∴AE⊥平面PCD.
(3)由(2)可知:AE⊥平面PCD.
∴∠ACE即为直线AC与平面PCD所成的角.
不妨设AD=2.
则AE=
| 3 |
| 2 |
∴sin∠ACE=
| AE |
| AC |
| ||
| 4 |

练习册系列答案
相关题目