题目内容
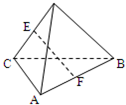
空间四边形ABCD中,M,N分别是AB和CD的中点,AD=BC=6,MN=3
,则AD和BC所成的角是( )
| 2 |
| A.120° | B.90° | C.60° | D.30° |
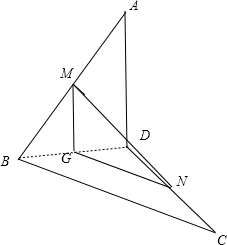
如图所示:取BD的中点G,连接GM,GN.空间四边形ABCD中,AD=BC=6,M、N分别是AB、CD的中点,
故MG是三角形ABD的中位线,GN是三角形CBD的中位线,
故∠MGN(或其补角)即为AD与BC所成的角.
△MGN中,MN=3
,MG=NG=3,
∴MG2+NG2=18=MN2,
∴∠MGN=90°.
故选B.
故MG是三角形ABD的中位线,GN是三角形CBD的中位线,
故∠MGN(或其补角)即为AD与BC所成的角.
△MGN中,MN=3
| 2 |
∴MG2+NG2=18=MN2,
∴∠MGN=90°.
故选B.


练习册系列答案
相关题目