题目内容
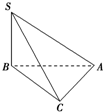 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:①异面直线SB与AC所成的角为90°.
②直线SB⊥平面ABC;
③平面SBC⊥平面SAC;
④点C到平面SAB的距离是
| 1 |
| 2 |
其中正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:平面与平面垂直的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:由条件根据异面直线所成的角,直线和平面垂直的判定定理、性质定理,平面和平面垂直的判定定理,判断各个选项是否正确,从而得出结论.
解答:
解:由题意知AC⊥平面SBC,故AC⊥SB,故①正确;
再根据SB⊥AC、SB⊥AB,可得SB⊥平面ABC,平面SBC⊥平面SAC,故②③正确;
取AB的中点E,连接CE,可证得CE⊥平面SAB,故CE的长度即为C到平面SAB的距离
a,④正确,
故选:D.
再根据SB⊥AC、SB⊥AB,可得SB⊥平面ABC,平面SBC⊥平面SAC,故②③正确;
取AB的中点E,连接CE,可证得CE⊥平面SAB,故CE的长度即为C到平面SAB的距离
| 1 |
| 2 |
故选:D.
点评:本题主要考查异面直线所成的角,直线和平面垂直的判定定理、性质定理,平面和平面垂直的判定定理的应用,体现了转化的数学思想,属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.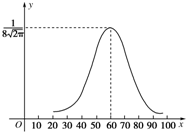 某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是
某校1000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(53,68]的人数大约是