题目内容
已知椭圆C的中心为原点,以坐标轴为对称轴,且经过(-
,
),(
,
)两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A(0,1)的直线l交椭圆C于M、N两点,若OM⊥ON,求直线l的方程.
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A(0,1)的直线l交椭圆C于M、N两点,若OM⊥ON,求直线l的方程.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设出椭圆的标准方程,将(-
,
),(
,
)代入构造方程组,从而求得椭圆C的标准方程.
(Ⅱ)设过点A(0,1)的直线l与椭圆C交于M(x1,y1),N(x2,y2),把直线代入椭圆的方程,再利用韦达定理求得 x1+x2 和x1•x2.根据OM⊥ON,即
•
=0,求得k的值.根可得直线l的方程.
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
(Ⅱ)设过点A(0,1)的直线l与椭圆C交于M(x1,y1),N(x2,y2),把直线代入椭圆的方程,再利用韦达定理求得 x1+x2 和x1•x2.根据OM⊥ON,即
| OM |
| ON |
解答:
解:(Ⅰ)设椭圆的方程为mx2+ny2=1,(m>0,n>0,m≠n),
∵椭圆C经过(-
,
),(
,
)两点,
∴
,
解得:
∴椭圆C的标准方程为
+x2=1.
(Ⅱ)由题意知,直线l的斜率存在,
设直线l与椭圆C交于M(x1,y1),N(x2,y2)两点,
由
,可得 (k2+4)x2+2kx-3=0,
∴x1+x2=-
,x1•x2=-
.
∵OM⊥ON,
∴
•
=0,
即 x1•x2+y1•y2=0,即(1+k2)x1•x2+k(x1+x2)+1=0,
即 (1+k2)(
)+k(
)+1=0,化间得-4k2+1=0,解得k=±
.
故直线l的方程为:y=±
x+1,即x-2y+2=0,或x+2y-2=0.
∵椭圆C经过(-
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
∴
|
解得:
|
∴椭圆C的标准方程为
| y2 |
| 4 |
(Ⅱ)由题意知,直线l的斜率存在,
设直线l与椭圆C交于M(x1,y1),N(x2,y2)两点,
由
|
∴x1+x2=-
| 2k |
| k2+4 |
| 3 |
| k2+4 |
∵OM⊥ON,
∴
| OM |
| ON |
即 x1•x2+y1•y2=0,即(1+k2)x1•x2+k(x1+x2)+1=0,
即 (1+k2)(
| -3 |
| k2+4 |
| -2k |
| k2+4 |
| 1 |
| 2 |
故直线l的方程为:y=±
| 1 |
| 2 |
点评:本题主要考查椭圆的标准方程,直线和圆锥曲线的位置关系的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设F1,F2为双曲线C:
-
=1(a>0,b>0)的左、右焦点,过坐标原点O的直线与双曲线C在第一象限内交于点P,若|PF1|+|PF2|=6a,且△PF1F2为锐角三角形,则直线OP斜率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||||||
B、(
| ||||||
C、(1,
| ||||||
D、(
|
已知sin(3π+α)=lg
,则tan(π+α)的值是( )
| 1 | |||
|
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
| A、(-5,-3)∪(-1,0) | ||||
B、(-5,-2)∪(-
| ||||
C、(-5,-
| ||||
D、(-
|
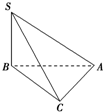 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: