题目内容
在数列{an}中,a1=1,Sn为数列{an}的前n项和,且满足
=1(n≥2)
(1)判断数列{
}是否为等差数列,并说明理由;
(2)并求数列{an}的通项公式;
(3)设bn=
,令Tn=
+
+…+
,若Tn<m对n≥2恒成立,求实数m的取值范围.
| 2an | ||
anSn-
|
(1)判断数列{
| 1 |
| Sn |
(2)并求数列{an}的通项公式;
(3)设bn=
|
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
考点:数列与不等式的综合,等差关系的确定
专题:计算题,等差数列与等比数列,不等式的解法及应用
分析:(1)运用数列的通项和前n项和的关系,化简整理,即可得到
-
=
,再由等差数列的定义,即可得到;
(2)运用等差数列的通项公式,注意n=1的情况,即可得到通项;
(3)求出数列bn=
,考虑Tn+1-Tn,化简整理得到大于0,有n≥2时,T2取得最小值,求出最小值,令m小于它即可.
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| 2 |
(2)运用等差数列的通项公式,注意n=1的情况,即可得到通项;
(3)求出数列bn=
|
解答:
解:(1)当n≥2时,2an=anSn-Sn2,an=Sn-Sn-1,
即有2(Sn-Sn-1)=Sn(Sn-Sn-1)-Sn2=-SnSn-1.
则有
-
=
,
则数列{
}为等差数列,且首项为1,公差为
;
(2)由等差数列的通项公式可得,
=1+
(n-1)=
,
即有Sn=
,
当n=1时,a1=1,当n>1时,an=Sn-Sn-1=
-
=
则an=
;
(3)bn=
,即为bn=
则Tn=
+
+…+
=
+
+…+
,
Tn+1=
+
+…+
+
+
,
Tn+1-Tn=
+
+
-
-
=
-
>0,
即有n≥2时,T2取得最小值,
则若Tn>m对n≥2恒成立可化为T2>m,
又∵T2=
+
=
,
则m<
.
即有2(Sn-Sn-1)=Sn(Sn-Sn-1)-Sn2=-SnSn-1.
则有
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| 2 |
则数列{
| 1 |
| Sn |
| 1 |
| 2 |
(2)由等差数列的通项公式可得,
| 1 |
| Sn |
| 1 |
| 2 |
| n+1 |
| 2 |
即有Sn=
| 2 |
| n+1 |
当n=1时,a1=1,当n>1时,an=Sn-Sn-1=
| 2 |
| n+1 |
| 2 |
| n |
| -2 |
| n(n+1) |
则an=
|
(3)bn=
|
|
则Tn=
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
| 1 |
| 1+n |
| 1 |
| 3+n |
| 1 |
| 2n+1 |
Tn+1=
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| 2n+3 |
Tn+1-Tn=
| 1 |
| 2n+2 |
| 1 |
| 2n+3 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+3 |
| 1 |
| (n+2)(n+3) |
| 1 |
| (2n+2)(2n+3) |
即有n≥2时,T2取得最小值,
则若Tn>m对n≥2恒成立可化为T2>m,
又∵T2=
| 1 |
| 3 |
| 1 |
| 5 |
| 8 |
| 15 |
则m<
| 8 |
| 15 |
点评:本题考查数列的通项和前n项和的关系,考查等差数列的通项公式,考查数列的单调性和运用:解决恒成立问题,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知角α终边上一点A的坐标为(-2,2
),则sinα=( )
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
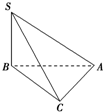 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: