题目内容
数列 的前n项和为
的前n项和为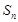 ,
, ,且对任意的
,且对任意的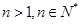 均满足
均满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.
 的前n项和为
的前n项和为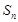 ,
, ,且对任意的
,且对任意的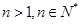 均满足
均满足 .
.(1)求数列
 的通项公式;
的通项公式; (2)若
 ,
, ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.(1)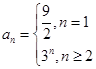 ;(2)
;(2)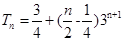
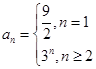 ;(2)
;(2)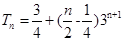
试题分析:(1)涉及
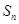 与
与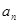 的递推式,往往有两种处理办法,转化为
的递推式,往往有两种处理办法,转化为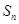 的递推式,或者转化为
的递推式,或者转化为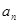 的递推式.本题
的递推式.本题 与
与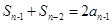 作差,得
作差,得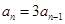 ,
,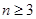 ,又
,又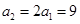 ,故
,故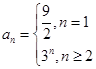
(2)求数列前n项和,首先研究其通项公式,根据通项公式的不同形式,选择相应的求和方法.本题中,
 ,故考虑错位相减法求和方法,
,故考虑错位相减法求和方法,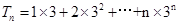 ,
,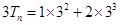
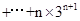 ,两式作差即可求
,两式作差即可求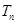 .
.(1)

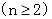 ①,
①,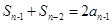
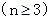 ②,①-②得,
②,①-②得, ,即
,即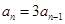 ,
,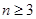 ,所以数列
,所以数列 从第二项开始是公比为3的等比数列,
从第二项开始是公比为3的等比数列,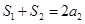 ,
,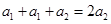
,
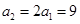 ,故当
,故当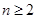 时,
时,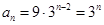 ,所以
,所以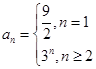 .
.(2)
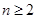 时,
时,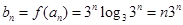 ;又
;又 ,故
,故 .
.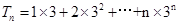 ,
,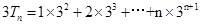 ,两式作差得,
,两式作差得,
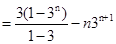 ,所以
,所以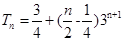 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,则
,则 的值为 ( )
的值为 ( ) 中各项均为正,有
中各项均为正,有 ,
,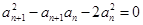 ,
, 中,
中, ,点
,点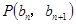 在直线
在直线 上.
上. 和
和 的值;(2)求数列
的值;(2)求数列 和
和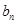 ;
; ,求数列
,求数列 的前n项和
的前n项和 .
. 满足奇数项
满足奇数项 成等差数列
成等差数列 ,而偶数项
,而偶数项 成等比数列
成等比数列 ,且
,且 ,
, 成等差数列,数列
成等差数列,数列 项和为
项和为 .
. ;
;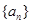 中,
中,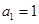 ,对于任意
,对于任意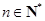 ,都有
,都有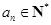 ,
,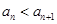 . 设
. 设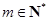 , 记使得
, 记使得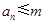 成立的
成立的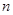 的最大值为
的最大值为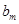 .
.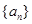 为1,3,5,7,
为1,3,5,7,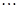 ,写出
,写出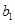 ,
,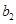 ,
,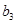 的值;
的值;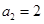 ,求
,求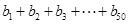 的值;
的值;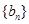 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列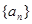 中,
中,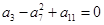 ,数列
,数列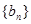 是等比数列,且
是等比数列,且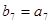 ,则
,则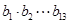 等于 .
等于 .