Question

6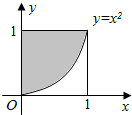．如图所示，曲线y=x²与y轴、直线y=1围成区域A（图中阴影部分），用模拟的方法求图中阴影部分的面积．（用两种方法）

Answer 1

分析 方法一：先由计算器做模拟试验结果试验估计，满足条件b＜a²的点（a，b）的概率，再转化为几何概型的面积类型求解，
方法二，根据定积分的几何意义即可求出．

解答 解：方法一：（1）利用计算机分别产生[0，1]和[0，1]上的均匀随机数：a=Rand和b=Rand，得随机数组（a，b）．
（2）统计试验总次数N和落在“曲边梯形”内的点数N₁（满足b＜a²的点（a，b）数）
（3）计算频率$\frac{N}{{N}_{1}}$得点落在“曲边梯形”上的概率近似值．
（4）由几何概型得p=$\frac{S}{1}$，所以$\frac{N}{{N}_{1}}$=$\frac{S}{1}$，于是得到S=$\frac{N}{N}$，这就是“曲边梯形”面积的近似值，
方法二：S_阴影=S_正方形-${∫}_{0}^{1}$x²dx=1×1-$\frac{1}{3}{x}^{3}$|${\;}_{0}^{1}$=1-$\frac{1}{3}$=$\frac{2}{3}$．

点评 本题考查模拟方法估计概率，考查几何概型，是一个比较好的题目，古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积和体积的比值得到．