题目内容
16．对四位数$\overline{abcd}$（1≤a≤9，0≤b，c，d≤9），若a＞b，b＜c，c＞d，则称$\overline{abcd}$为P类数；若a＜b，b＞c，c＜d，则称$\overline{abcd}$为Q类数，用N（P）与N（Q）分别表示P类数与Q类数的个数，则N（P）-N（Q）的值为285．分析 对于一个四位数abcd，则dcba为其回文数，显然，一个末尾不为0的P类数，其回文数为一个Q类数；而一个Q类数的回文数为一个P类数，故Q类数与末尾不为0的P类数构成一一对应，其个数相等，于是可知N（P）-N（Q）为末尾为0的P类数的个数，即可得出结论．
解答 解：对于一个四位数abcd，则dcba为其回文数，显然，一个末尾不为0的P类数，其回文数为一个Q类数；而一个Q类数的回文数为一个P类数，故Q类数与末尾不为0的P类数构成一一对应，其个数相等，于是可知N（P）-N（Q）为末尾为0的P类数的个数，末尾为0的P类数构成的集合为S={abc0|a，b，c∈Z，9≥a＞b≥0，0≤b＜c≤9}，于是N（P）-N（Q）的值为92+82+…+12=285．
故答案为：285．
点评 本题考查学生利益数学知识解决实际问题的能力，考查学生分析解决问题的能力，确定Q类数与末尾不为0的P类数构成一一对应，其个数相等，于是可知N（P）-N（Q）为末尾为0的P类数的个数是关键．
练习册系列答案
备战中考寒假系列答案
相关题目
4．已知x-3=8，那么x等于（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | $\frac{1}{2}$ |
11．某产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
（1）求线性回归方程；
（2）预测当广告费支出7（百万元）时的销售额．
附：$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$．
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（2）预测当广告费支出7（百万元）时的销售额．
附：$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$．
8．设U为全集，A，B是集合，若存在集合C使得A⊆C，B⊆∁UC，则下列集合中必为空集是（ ）
| A． | A∩B | B． | （∁UA）∩C | C． | （∁UB）∩（∁UC） | D． | （∁UC）∩B |
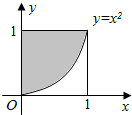如图所示，曲线y=x2与y轴、直线y=1围成区域A（图中阴影部分），用模拟的方法求图中阴影部分的面积．（用两种方法）