题目内容
1.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)在区间[-ω,ω]上单调递增,且函数f(x)的图象关于x=ω对称,则ω的值$\frac{\sqrt{3π}}{3}$.分析 由条件利用两角和的正弦公式化简函数的解析式,再利用正弦函数的单调性和图象的对称性求得ω2+$\frac{π}{6}$=$\frac{π}{2}$,由此求得ω的值.
解答 解:∵函数f(x)=$\sqrt{3}$sinωx+cosωx=2sin(ωx+$\frac{π}{6}$)(ω>0)的图象关于x=ω对称,
∴ω2+$\frac{π}{6}$=kπ+$\frac{π}{2}$(k∈Z),∴ω2=kπ+$\frac{π}{3}$(k∈Z),
f(x)在区间[-ω,ω]上单调递增,∴半个周期大于或等于2ω,即$\frac{π}{ω}$≥2ω,∴ω2≤$\frac{π}{2}$,
∴应有ω2=$\frac{π}{3}$,求得ω=$\frac{\sqrt{3π}}{3}$,
故答案为:$\frac{\sqrt{3π}}{3}$.
点评 本题主要考查两角和的正弦公式、正弦函数的单调性和图象的对称性,属于基础题.

练习册系列答案
相关题目
11.某产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
(1)求线性回归方程;
(2)预测当广告费支出7(百万元)时的销售额.
附:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)预测当广告费支出7(百万元)时的销售额.
附:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$.
10.在平行四边形ABCD中,$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),则四边形ABCD的面积为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
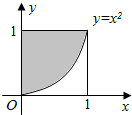 如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)
如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)