题目内容
11.已知f(x)是定义在区间[-1,1]上的奇函数,且f(1)=1,当a,b∈[-1,1],a+b≠0时,有$\frac{f(a)+f(b)}{a+b}$>0.(1)判断函数f(x)在其定义域上是增函数还是减函数.并证明你的结论;
(2)若把定义域与值域相同的函数叫做“同域函数”,判断函数f(x)是否是“同域函数”.
分析 (1)函数f(x)在[-1,1]上是增函数,用单调性的定义即可证明;
(2)根据(1)的结论,求出函数f(x)在[-1,1]上的值域,判断f(x)是否为“同域函数”即可.
解答 解:(1)函数f(x)在[-1,1]上是增函数,证明如下:
任取x1,x2∈[-1,1],且x1<x2,则x2-x1>0,
即x2+(-x1)>0,其中-x1,x2∈[-1,1],
∴$\frac{f{(x}_{2})+f({-x}_{1})}{{x}_{2}+({-x}_{1})}$>0,
∴f(x2)+f(-x1)>0;
又f(x)是[-1,1]上的奇函数,
∴f(-x1)=-f(x1),
∴f(x2)-f(x1)>0,
即f(x1)<f(x2);
∴函数f(x)在[-1,1]上是增函数;
(2)由(1)知,函数f(x)在[-1,1]上是增函数,
且f(1)=1;
又f(x)是定义在区间[-1,1]上的奇函数,
∴f(-1)=-f(1)=-1,
∴f(x)的值域为[-1,1],
∴函数f(x)的定义域与值域相同,是“同域函数”.
点评 本题考查了新定义的函数的奇偶性与单调性的判断与证明问题,是综合性题目.

练习册系列答案
相关题目
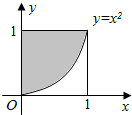 如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)
如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)