题目内容
17.已知数列{an}的前n项和为Sn,且满足an=$\frac{1}{2}$Sn+1(n∈N*);(1)求数列{an}的通项公式;
(2)若bn=log2an,cn=$\frac{1}{{b}_{n}{b}_{n+2}}$,求证数列{cn}的前n项和为Tn<$\frac{3}{4}$.
分析 (1)利用递推关系及其等比数列的通项公式即可得出;
(2)bn=log2an=n.cn=$\frac{1}{{b}_{n}{b}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用“裂项求和”即可得出.
解答 (1)解:∵满足an=$\frac{1}{2}$Sn+1(n∈N*),
∴当n=1时,${a}_{1}=\frac{1}{2}{a}_{1}$+1,解得a1=2.
当n≥2时,${a}_{n-1}=\frac{1}{2}{S}_{n-1}$+1,
∴an-an-1=$\frac{1}{2}{a}_{n}$,化为an=2an-1.
∴数列{an}是等比数列,首项为2,公比为2.
∴an=2n.
(2)证明:bn=log2an=n.
cn=$\frac{1}{{b}_{n}{b}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴数列{cn}的前n项和为Tn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})+(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$<$\frac{3}{4}$.
点评 本题考查了递推关系、等比数列的通项公式、“裂项求和”、不等式的性质、“放缩法”,考查了推理能力与计算能力,属于中档题.

 小题狂做系列答案
小题狂做系列答案| A. | A∩B | B. | (∁UA)∩C | C. | (∁UB)∩(∁UC) | D. | (∁UC)∩B |
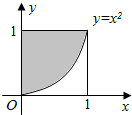 如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)
如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)