题目内容
18.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosB=$\frac{3}{5}$,a=5$\sqrt{3}$.(1)若A=60°,求b的值;
(2)若函数f(x)=x2-7$\sqrt{3}$x+m的两零点分别为b,c,求m的值.
分析 (1)先求sinB的值,由正弦定理可得b的值.
(2)由韦达定理可得:8+c=7$\sqrt{3}$①,8c=m②,即可解得m的值.
解答 解:(1)∵cosB=$\frac{3}{5}$,B∈(0,π),
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{4}{5}$,
∵a=5$\sqrt{3}$,A=60°,
∴由正弦定理可得:b=$\frac{asinB}{sinA}$=$\frac{5\sqrt{3}×\frac{4}{5}}{\frac{\sqrt{3}}{2}}$=8.
(2)∵函数f(x)=x2-7$\sqrt{3}$x+m的两零点分别为b,c,
∴8+c=7$\sqrt{3}$①,8c=m②,
∴由①②可解得:c=7$\sqrt{3}-8$,m=56$\sqrt{3}$-64.
点评 本题主要考查了同角三角函数关系式的应用,考查了正弦定理,韦达定理的应用,属于基本知识的考查.

练习册系列答案
相关题目
8.设U为全集,A,B是集合,若存在集合C使得A⊆C,B⊆∁UC,则下列集合中必为空集是( )
| A. | A∩B | B. | (∁UA)∩C | C. | (∁UB)∩(∁UC) | D. | (∁UC)∩B |
10.在平行四边形ABCD中,$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),则四边形ABCD的面积为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
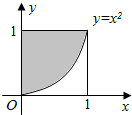 如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)
如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)