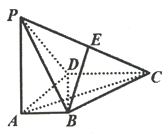
题目内容
【题目】已知
，
分别是双曲线
的左顶点、右焦点，过的直线
与
的一条渐近线垂直且与另一条渐近线和
轴分别交于
，
两点.若
，则的离心率是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由已知条件设出直线l的方程，与y＝﹣
x联立，求P点坐标，将x＝0带入直线l，求Q点坐标，由AP⊥AQ，知kAPkAQ，由此求离心率．
∵A，F分别是双曲线
的左顶点、右焦点，
∴A（﹣a，0）F（c，0），
∵过F的直线l与C的一条渐近线垂直，
且与另一条渐近线和y轴分别交于P，Q两点，
∴直线l的方程为：y＝﹣
，
直线l：y＝﹣与y＝﹣x联立：
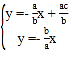，解得P点
将x＝0带入直线l：y＝﹣，得Q（0，
），
∵AP⊥AQ，∴kAPkAQ＝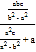
×
＝﹣1，
化简得b2﹣ac﹣a2＝﹣c2，
把b2＝c2﹣a2代入，得2c2﹣2a2﹣ac＝0
同除a2得2e2﹣2﹣e＝0，
∴e＝
，或e＝
（舍）．
故选：D．
练习册系列答案
相关题目
【题目】某工厂生产甲、乙两种产品所得的利润分别为
和
（万元），事先根据相关资料得出它们与投入资金
（万元）的数据分别如下表和图所示：其中已知甲的利润模型为
，乙的利润模型为
．（
为参数，且
）.
|
|
|
|
|
|
|
|
|
|
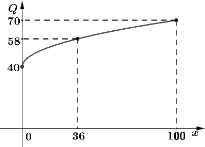
（1）请根据下表与图中数据，分别求出甲、乙两种产品所得的利润与投入资金（万元）的函数模型
（2）今将
万资金投入生产甲、乙两种产品，并要求对甲、乙两种产品的投入资金都不低于
万元．设对乙种产品投入资金
（万元），并设总利润为
（万元），如何分配投入资金，才能使总利润最大？并求出最大总利润．
