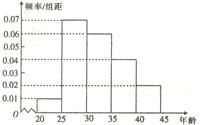
题目内容
【题目】(1)讨论函数f(x)=![]() ex的单调性,并证明当x>0时,(x-2)ex+x+2>0.
ex的单调性,并证明当x>0时,(x-2)ex+x+2>0.
(2)证明:当a∈[0,1) 时,函数g(x)=![]() (x>0) 有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.
(x>0) 有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.
【答案】(1)在![]() 和
和![]() 上都是递增,证明见解析;(2)证明见解析,
上都是递增,证明见解析;(2)证明见解析,![]() .
.
【解析】试题分析:(1)求导后分析导数大于零(或小于零)的解,即可求出单调区间,利用极小值即可证明不等式成立;(2)利用二次求导求函数的单调性最值,从而求出h(a)的值域.
试题解析:
(1)f(x)=![]() ex,x∈(-∞,-2)∪(-2,+∞).
ex,x∈(-∞,-2)∪(-2,+∞).
f ′(x)=ex![]() =
=![]() ,
,
因为当x∈(-∞,-2)∪(-2,+∞)时,f ′(x)>0,
所以f(x)在(-∞,-2)和(-2,+∞)上单调递增,
所以x>0时,![]() ex>f(0)=-1,
ex>f(0)=-1,
所以(x-2)ex+x+2>0.
(2)g′(x)=![]()
=![]()
=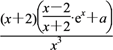 ,a∈[0,1).
,a∈[0,1).
由(1)知,当x>0时,f(x)=![]() ·ex的值域为(-1,+∞),只有一解,使得
·ex的值域为(-1,+∞),只有一解,使得![]() ·et=-a,t∈(0,2].
·et=-a,t∈(0,2].
当x∈(0,t)时g′(x)<0,g(x)单调递减;
当x∈(t,+∞)时g′(x)>0,g(x)单调递增.
h(a)=![]() =
=![]() =
=![]() ,
,
记k(t)=![]() ,在t∈(0,2]时,k′(t)=
,在t∈(0,2]时,k′(t)=![]() >0,
>0,
所以k(t)单调递增,
所以h(a)=k(t)∈![]() .
.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目