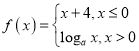题目内容
【题目】(本题满分12分)
已知椭圆
的中心在原点，焦点在
轴上，椭圆上的点到焦点的距离的最
小值为
，离心率为
。
（I）求椭圆
的方程；
（Ⅱ）过点（1，0）作直线
交
于
、
两点，试问：在
轴上是否存在一个定点
，使
为定值？若存在，求出这个定点
的坐标；若不存在，请说明理由。
【答案】
解：（I）设椭圆E的方程为
由已知得：
2分
椭圆E的方程为
················································3分
（Ⅱ）解：假设存在符合条件的点
，又设
，则：
···················································5分
①当直线
的斜率存在时，设直线
的方程为：
，则
由
得
7分
所以
·················································9分
对于任意的
值，
为定值，
所以
，得
，
所以
；······················································11分
②当直线
的斜率不存在时，直线
由
得
综上述①②知，符合条件的点
存在，起坐标为
。························12分
【解析】略
口算小状元口算速算天天练系列答案
【题目】在创建“全国文明卫生城”过程中，某市“创城办”为了调查市民对创城工作的了解情况，进行了一次创城知识问卷调查(一位市民只能参加一次).通过随机抽样，得到参加问卷调查的1000人的得分(满分100分)统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
（1）由频数分布表可以大致认为，此次问卷调查的得分
服从正态分布
， 
近似为这1000人得分的平均值值(同一组数据用该组数据区间的中点值表示)，请用正态分布的知识求
；
（2）在（1）的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案：:
（ⅰ）得分不低于
的可以获赠2次随机话费，得分低于
的可以获赠1次随机话费；
（ⅱ）每次获赠送的随机话费和对应的概率为：
赠送的随机话费（单元：元） | 20 | 40 |
概率 | 0.75 | 0.25 |
现有市民甲要参加此次问卷调查，记
(单位：元)为该市民参加问卷调查获赠的话费,求
的分布列与数学期望.
附：参考数据与公式
，若
，则
①
；
②
；
③
.
