题目内容
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆C的方程;
(2)过点(1,0)作直线l与圆C交于A,B两点,O是坐标原点,是否存在直线l,使得∠AOB=90°?若存在,求出所有满足条件的直线l的方程;若不存在,请说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(Ⅰ)求出圆心![]() 关于直线l1的对称点得到圆C的圆心坐标,即可得答案;(Ⅱ)通过经过直线l与圆C1的圆的圆心在AB上,且经过原点,列方程解得.
关于直线l1的对称点得到圆C的圆心坐标,即可得答案;(Ⅱ)通过经过直线l与圆C1的圆的圆心在AB上,且经过原点,列方程解得.
解:(Ⅰ) 圆C1化为标准方程为(x-1)2+y2=9,
设圆心![]() (1,0)关于直线l1:y=x+1的对称点为C(a,b),
(1,0)关于直线l1:y=x+1的对称点为C(a,b),
则![]() ,且CC1的中点
,且CC1的中点![]() 在直线l1:y=x+1上,
在直线l1:y=x+1上,
∴有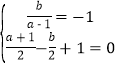 ,解得:
,解得:![]() ,
,
∴圆C的方程为![]() ,
,
(Ⅱ)假设存在直线l,显然直线l有斜率,设直线![]() ,
,
设经过直线l和圆C的圆的方程为:![]()
即![]() ,
,
依题意该圆过原点且圆心在直线l上,
∴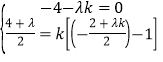 解得λ=-4,k=1,
解得λ=-4,k=1,
所以存在直线![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
