题目内容
【题目】已知二次函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设函数![]() ,记
,记![]() 为函数
为函数![]() 极大值点,求证:
极大值点,求证: ![]() .
.
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:(1)求出函数的导数,通过讨论![]() 的范围,求出函数的单调区间即可;
的范围,求出函数的单调区间即可;
(2)由题![]()
则![]() ,此时
,此时![]() ,讨论
,讨论![]() 的单调性可得,
的单调性可得, ![]() 在
在![]() 处取得极大值
处取得极大值![]() ,则
,则![]() 一定有
一定有![]() 个零点,分别是
个零点,分别是![]() 的极大值点和极小值点.
的极大值点和极小值点.
设![]() 是函数
是函数![]() 的一个极大值点,则
的一个极大值点,则![]()
所以, ![]() ,由
,由![]() 所以,
所以, ![]()
此时![]() 可证明
可证明![]() .
.
试题解析:(1)![]()
![]()
当![]() 时,
时, ![]() 在
在![]() 上恒正;
上恒正;
所以, ![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,由
时,由![]() 得
得![]() ,
,
所以当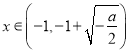 时,
时, ![]() 单调递减
单调递减
当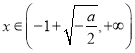 时,
时, ![]() 单调递增.
单调递增.
综上所述,
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,
当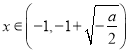 时,
时, ![]() 单调递减;
单调递减;
当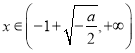 时,
时, ![]() 单调递增.
单调递增.
(2)![]()
则![]()
![]()
令![]() 的
的![]()
当![]() 时,
时, ![]() 为增函数;
为增函数;
当![]() 时,
时, ![]() 为减函数;
为减函数;
所以, ![]() 在
在![]() 处取得极大值
处取得极大值![]() ,
,
![]() 一定有
一定有![]() 个零点,分别是
个零点,分别是![]() 的极大值点和极小值点.
的极大值点和极小值点.
设![]() 是函数
是函数![]() 的一个极大值点,则
的一个极大值点,则![]()
所以, ![]()
又![]()
所以, ![]()
此时![]()
所以![]() .
.

【题目】某地区某农产品近几年的产量统计如表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
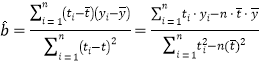 ,
,![]()
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2019(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
【题目】下表数据为某地区某种农产品的年产量![]() (单位:吨)及对应销售价格
(单位:吨)及对应销售价格![]() (单位:千元/吨).
(单位:千元/吨).
| 1 | 2 | 3 | 4 | 5 |
| 70 | 65 | 55 | 38 | 22 |
(1)若![]() 与
与![]() 有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出
有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润![]() 最大?
最大?
(参考公式:回归直线方程为![]() ,其中
,其中 )
)



