题目内容
【题目】定义:若数列![]() 和
和![]() 满足
满足![]() 则称数列
则称数列![]() 是数列
是数列![]() 的“伴随数列”.
的“伴随数列”.
已知数列![]() 是数列
是数列![]() 的伴随数列,试解答下列问题:
的伴随数列,试解答下列问题:
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若![]() ,
,![]() 为常数,求证:数列
为常数,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,数列
,数列![]() 是等比数列,求
是等比数列,求![]() 的数值.
的数值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3) .
.
【解析】试题分析:(1)根据题意,由![]() ,
,![]() ,代入
,代入![]() .
.
可求得![]() ,
,![]() .
.
(2)由 ![]() ,代入
,代入![]() ,
,
可得![]() ,
,![]() .即可证明数列
.即可证明数列![]() 是首项为
是首项为![]() 公差为
公差为![]() 的等差数列.
的等差数列.
(3).由题意可得)![]() . 由
. 由![]() 是等比数列,且
是等比数列,且![]() ,设公比为
,设公比为![]() ,则
,则![]() .
.
可证明当![]() , 和
, 和![]() 时均不成立.故
时均不成立.故 ![]() ,
,![]() (
(![]() ).
).
根据数列![]() 是等比数列,有
是等比数列,有![]() .
.![]() .根据
.根据
![]() 可化为
可化为
![]() ,
,![]() . 可知关于
. 可知关于![]() 的一元二次方程
的一元二次方程![]() 有且仅有两个非负实数根.可证明
有且仅有两个非负实数根.可证明![]() ,
,![]() ,
,![]() . 由
. 由![]() ,得
,得![]() . 把
. 把![]() ,代入
,代入![]() 可得
可得![]() ..
..
试题解析:(1)根据题意,有![]() .
.
由![]() ,
,![]() ,得
,得
![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
(2) ![]()
![]() ,
,![]() ,
,
∴ ,
, ,/span>
,/span>![]() .
.
∴![]() ,
,![]() .
.
∴数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列.
的等差数列.
(3) ![]()
![]() ,
, ![]() ,
,
由![]() ,得
,得![]() .
.
![]()
![]() 是等比数列,且
是等比数列,且![]() ,设公比为
,设公比为![]() ,则
,则![]() .
.
∴当![]() ,即
,即![]() ,与
,与![]() 矛盾.因此,
矛盾.因此,![]() 不成立.
不成立.
当![]() ,即
,即![]() ,与
,与![]() 矛盾.因此,
矛盾.因此,![]() 不成立.
不成立.
![]()
![]() ,即数列
,即数列![]() 是常数列,于是,
是常数列,于是,![]() (
(![]() ).
).
![]() .
.
![]() ,数列
,数列![]() 也是等比数列,设公比为
也是等比数列,设公比为![]() ,有
,有![]() .
.
![]() 可化为
可化为
![]() ,
,![]() .
.
![]()
![]() ,
,
![]() 关于
关于![]() 的一元二次方程
的一元二次方程![]() 有且仅有两个非负实数根.
有且仅有两个非负实数根.
一方面,![]() (
(![]() )是方程
)是方程![]() 的根;另一方面,
的根;另一方面,
若![]() ,则无穷多个互不相等的
,则无穷多个互不相等的![]() 都是该二次方程的根.这与该二次方程有且仅有两个非负实数根矛盾!
都是该二次方程的根.这与该二次方程有且仅有两个非负实数根矛盾!
![]() ,即数列
,即数列![]() 也是常数列,于是,
也是常数列,于是,![]() ,
,![]() .
.
![]() 由
由![]() ,得
,得![]() .
.
把![]() ,代入
,代入![]() 解得
解得![]() .
.  .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限![]() 与所支出的总费用
与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1) 在给出的坐标系中作出散点图;
(2)求线性回归方程![]() 中的
中的![]() 、
、![]() ;
;
(3)估计使用年限为![]() 年时,车的使用总费用是多少?
年时,车的使用总费用是多少?
(最小二乘法求线性回归方程系数公式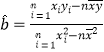 ,
, ![]() .)
.)

