题目内容
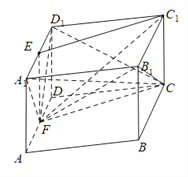
【题目】如图所示,一块形状为四棱柱的木料, ![]() 分别为
分别为![]() 的中点.
的中点.
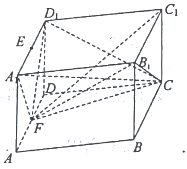
(1)要经过![]() 和
和![]() 将木料锯开,在木料上底面
将木料锯开,在木料上底面![]() 内应怎样画线?请说明理由;
内应怎样画线?请说明理由;
(2)若底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,
, ![]() 平面
平面![]() ,且
,且![]() ,求几何体
,求几何体![]() 的体积.
的体积.
【答案】(1)见解析(2)3
【解析】试题分析:(1)根据面面平行的性质,两个平行平面,被第三个平面所截,截得的交线互相平行,故得到![]() 就是应画的线;(2)几何体
就是应画的线;(2)几何体![]() 是由三棱锥
是由三棱锥![]() 和四棱锥
和四棱锥![]() 组成,分割成两个棱锥求体积即可。
组成,分割成两个棱锥求体积即可。
解析:
(1)连接![]() ,则
,则![]() 就是应画的线;
就是应画的线;
事实上,连接![]() ,在四棱柱
,在四棱柱![]() 中,
中,
因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ,
, ![]() ,
,
所以![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又在![]() 四棱柱中
四棱柱中![]() ,
,
所以![]() ,
,
所以点![]() 共面,
共面,
又![]() 面
面![]() ,所以
,所以![]() 就是应画线.
就是应画线.
(2)几何体![]() 是由三棱锥
是由三棱锥![]() 和四棱锥
和四棱锥![]() 组成.
组成.
因为底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
,
连接![]() ,
, ![]() 即为三棱锥
即为三棱锥![]() 的高,
的高,
又![]() ,所以
,所以![]() ,
,
连接![]() ,
, ![]() 为四棱锥
为四棱锥![]() 的高,
的高,
又![]() ,所以
,所以![]() ,
,
所以几何体![]() 的体积为
的体积为![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00﹣22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00﹣22:00时间段的休闲方式与性别有关系”?