题目内容
【题目】已知以点A（﹣1，2）为圆心的圆与直线m：x+2y+7=0相切，过点B（﹣2，0）的动直线l与圆A相交于M、N两点
（1）求圆A的方程．
（2）当|MN|=2 
时，求直线l方程．
【答案】
（1）解：意知A（﹣1，2）到直线x+2y+7=0的距离为圆A半径r，
∴ 
，
∴圆A方程为（x+1）2+（y﹣2）2=20
（2）垂径定理可知∠MQA=90°．且 
，
在Rt△AMQ中由勾股定理易知 
设动直线l方程为：y=k（x+2）或x=﹣2，显然x=﹣2合题意．
由A（﹣1，2）到l距离为1知 
．
∴3x﹣4y+6=0或x=﹣2为所求l方程．
【解析】（1）当直线与圆相切时，根据圆心到直线的距离等于半径列出等式，（2）根据垂径定理，由勾股定理算出AQ，设出动直线的方程再结合点到直线方程可求出.
练习册系列答案
名校课堂系列答案
相关题目
【题目】在
年初的时候，国家政府工作报告明确提出， 
年要坚决打好蓝天保卫战，加快解决燃煤污染问题，全面实施散煤综合治理.实施煤改电工程后，某县城的近六个月的月用煤量逐渐减少， 
月至
月的用煤量如下表所示：
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
（1）由于某些原因， 
中一个数据丢失，但根据
至
月份的数据得出
样本平均值是
，求出丢失的数据；
（2）请根据
至
月份的数据，求出
关于
的线性回归方程
；
（3）现在用（2）中得到的线性回归方程中得到的估计数据与
月
月的实际数据的误差来判断该地区的改造项目是否达到预期，若误差均不超过
，则认为该地区的改造已经达到预期，否则认为改造未达预期，请判断该地区的煤改电项目是否达预期？
（参考公式：线性回归方程
，其中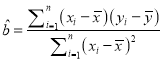
）
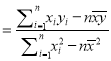