题目内容
【题目】已知极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同![]() 直线
直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() 为参数
为参数![]() ,设直线l与曲线C交于A,B两点.
,设直线l与曲线C交于A,B两点.
![]() 写出直线
写出直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
![]() 已知点P在曲线C上运动,求点P到直线
已知点P在曲线C上运动,求点P到直线![]() 距离的最大值.
距离的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
![]() 直线l的极坐标方程转化为
直线l的极坐标方程转化为![]() ,由此能求出直线l的普通方程;曲线C的参数方程消去参数
,由此能求出直线l的普通方程;曲线C的参数方程消去参数![]() ,能求出曲线C的直角坐标方程;联立
,能求出曲线C的直角坐标方程;联立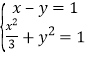 ,能求出线段AB的长;
,能求出线段AB的长;
![]() 设
设![]() ,点P到直线l距离:
,点P到直线l距离:![]() ,当
,当![]() 时,能求出点P到直线l距离取最大值.
时,能求出点P到直线l距离取最大值.
解:![]() 直线l的极坐标方程为
直线l的极坐标方程为![]() ,
,
即![]() ,
,
![]() 直线l的普通方程为
直线l的普通方程为![]() .
.
![]() 曲线C的参数方程为
曲线C的参数方程为![]() 为参数
为参数![]() ,
,
![]() 曲线C的直角坐标方程为
曲线C的直角坐标方程为![]() .
.
联立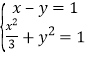 ,得
,得![]() .
.
解得![]() ,
,
![]() ,
,![]() ,
,
![]() 线段AB的长
线段AB的长![]() .
.
![]() 点P在曲线C上运动,
点P在曲线C上运动,![]() 设
设![]() ,
,
![]() 点P到直线l距离:
点P到直线l距离:![]() ,
,
![]() 当
当![]() 时,点P到直线l距离取最大值
时,点P到直线l距离取最大值![]() .
.

练习册系列答案
相关题目
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如表:
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:
(2)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
参考数据:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.