题目内容
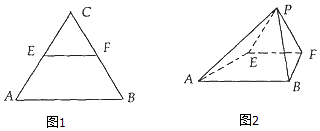
【题目】等腰△ABC中，AC=BC= 
，AB=2，E，F分别为AC，BC的中点，将△EFC沿EF折起，使得C到P，得到四棱锥P﹣ABFE，且AP=BP= 
． 
（1）求证：平面EFP⊥平面ABFE；
（2）求二面角B﹣AP﹣E的大小．
【答案】
（1）证明：在△ABC中，D为AB中点，O为EF中点．
由AC=BC= 
，AB=2．
∵E、F分别为AC、BC的中点，
∴EF为中位线，得CO=OD=1，CO⊥EF
∴四棱锥P﹣ABFE中，PO⊥EF，
∵OD⊥AB，AD=OD=1，∴AO= 
，
又AP= 
，OP=1，
∴四棱锥P﹣ABFE中，有AP2=AO2+OP2，即OP⊥AO，…4分
又AO∩EF=O，EF、AO平面ABFE，
∴OP⊥平面ABFE，
又OP平面EFP，
∴平面EFP⊥平面ABFE
（2）解：由（1）知OD，OF，OP两两垂直，以O为原点，建立空间直角坐标系（如图）：
则A（1，﹣1，0），B（1，1，0），E（0， 
，0），P（0，0，1）…7分
∴ 
， 
，
设 
， 
分别为平面AEP、平面ABP的一个法向量，
则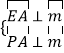 
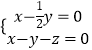取x=1，得y=2，z=﹣1
∴ 
．
同理可得 
由于 
=0，
所以二面角B﹣AP﹣E为90°．
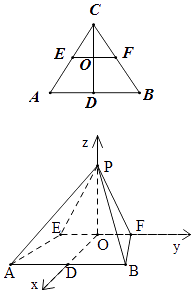
【解析】（1）用分析法找思路，用综合法证明．取EF中点O，连接OP、OC．等腰三角形CEF中有CO⊥EF，即OP⊥EF．根据两平面垂直的性质定理，平面PEF和平面ABFE的交线是EF，且PO⊥EF，分析得PO⊥平面ABFE．故只需根据题中条件证出PO⊥平面ABFE，即可利用面面垂直的判定定理证得平面EFP⊥平面ABFE．（2）根据第一问分析空间位置关系，可建立空间直角坐标线求得平面ABP和平面AEP的法向量的所成角，利用向量角和二面角关系，确定二面角大小．
