题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)将![]() ,
, ![]() 的方程化为普通方程,并说明它们分别表示什么曲线?
的方程化为普通方程,并说明它们分别表示什么曲线?
(2)以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .若
.若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 为
为![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
【答案】(1)![]() 表示以
表示以![]() 为圆心,1为半径的圆,
为圆心,1为半径的圆, ![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;(2)
轴上的椭圆;(2)![]() .
.
【解析】试题分析:(1)分别将曲线![]() 、
、![]() 的参数方程利用平方法消去参数,即可得到
的参数方程利用平方法消去参数,即可得到![]() ,
, ![]() 的方程化为普通方程,进而得到它们分别表示什么曲线;(2)
的方程化为普通方程,进而得到它们分别表示什么曲线;(2)![]() ,利用点到直线距离公式可得
,利用点到直线距离公式可得![]() 到直线
到直线![]() 的距离
的距离![]() ,利用辅助角公式以及三角函数的有界性可得结果.
,利用辅助角公式以及三角函数的有界性可得结果.
试题解析:(1)![]() 的普通方程为
的普通方程为![]() ,它表示以
,它表示以![]() 为圆心,1为半径的圆,
为圆心,1为半径的圆,
![]() 的普通方程为
的普通方程为![]() ,它表示中心在原点,焦点在
,它表示中心在原点,焦点在![]() 轴上的椭圆.
轴上的椭圆.
(2)由已知得![]() ,设
,设![]() ,则
,则![]() ,
,
直线![]() :
: ![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离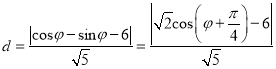 ,
,
所以![]() ,即
,即![]() 到
到![]() 的距离的最小值为
的距离的最小值为![]() .
.

练习册系列答案
相关题目