题目内容
7.设正四棱台ABCD-A′B′C′D′中的上、下底面边长分别为2和4,侧棱长度为2,求这个棱台的高和斜高.分析 正四棱台ABCD-A′B′C′D′中,作出上、下底的中心O、O′,连结OO′,过O作OE⊥AD,交AD于E,过O′作O′F⊥A′D′,交A′D′于F,过E作EK⊥O′F,交O′F于K,高h=OO'=EK,斜高 h'=EF=DH,由此能求出结果.
解答 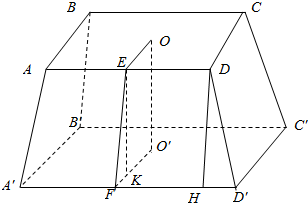 解:∵正四棱台ABCD-A′B′C′D′中的上、下底面边长分别为2和4,侧棱长度为2,
解:∵正四棱台ABCD-A′B′C′D′中的上、下底面边长分别为2和4,侧棱长度为2,
∴如图:正四棱台ABCD-A′B′C′D′中,
作出上、下底的中心O、O′,连结OO′,
过O作OE⊥AD,交AD于E,过O′作O′F⊥A′D′,交A′D′于F,
过E作EK⊥O′F,交O′F于K,
则高h=OO'=EK,
斜高 h'=EF=DH,HD′=$\frac{4-2}{2}$=1=KF,
斜高 h'=EF=DH=$\sqrt{4-1}$=$\sqrt{3}$,
高h=OO'=EK=$\sqrt{E{F}^{2}-F{K}^{2}}$=$\sqrt{3-1}$=$\sqrt{2}$.
∴这个棱台的高为$\sqrt{2}$,斜高为$\sqrt{3}$.
点评 本题考查正四棱台的高和斜高的求法,是基础题,解题时要认真审题,注意正四棱台的结构特征的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,a2=4,设数列{an}的前n项和为Sn,则数列{$\frac{1}{{S}_{n}}$}的前10项和为( )
| A. | $\frac{11}{12}$ | B. | $\frac{10}{11}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
16.数列{an}满足${a_n}-{({-1})^n}{a_{n-1}}=n,({n≥2})$,Sn是{an}的前n项和,则S40=( )
| A. | 880 | B. | 900 | C. | 440 | D. | 450 |
 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.