题目内容
16.数列{an}满足${a_n}-{({-1})^n}{a_{n-1}}=n,({n≥2})$,Sn是{an}的前n项和,则S40=( )| A. | 880 | B. | 900 | C. | 440 | D. | 450 |
分析 由已知得a4n-3=a1,a4n-2=4n-2+a1,a4n-1=1-a1,a4n=4n+1-a1,从而得到S40=a1+(a2+a3)+(a4+a5)+…+(a38+a39)+a40=a1+3+5+…+39+41-a1,由此能求出结果.
解答 解:∵数列{an}满足${a_n}-{({-1})^n}{a_{n-1}}=n,({n≥2})$,
∴a1=a1,
a2=2+a1,
a3=3-a2=1-a1,
a4=4+a3=5-a1,
a5=5-a4=a1,
a6=6+a5=6+a1,
a7=7-a6=1-a1,
a8=8+a7=9-a1,
a9=9-a8=a1,
…
a4n-3=a1,
a4n-2=4n-2+a1,
a4n-1=1-a1,
a4n=4n+1-a1,
∴S40=a1+(a2+a3)+(a4+a5)+…+(a38+a39)+a40
=a1+3+5+…+39+41-a1
=440.
故选:C.
点评 本题考查数列的前40项和的求法,是中档题,解题时要认真审题,注意数列的递推公式的合理运用.

练习册系列答案
相关题目
11.由直线x=1,x=2,y=0与曲线y=$\frac{1}{x}$所围成的曲边梯形,将区间[1,2]等分成4份,将曲边梯形较长的边近似看作高,则曲边梯形的面积是( )
| A. | $\frac{9}{20}$ | B. | $\frac{37}{60}$ | C. | $\frac{319}{420}$ | D. | $\frac{259}{420}$ |
1.f(x)=$\left\{\begin{array}{l}{x+2,}&{x≤-1}\\{{x}^{2},}&{-1<x<2}\\{2x,}&{x≥2}\end{array}\right.$,若f(x0)=3,则x0=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
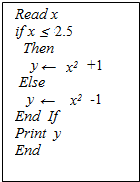 若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.
若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.