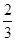题目内容
若二项式(
+x2)3展开式中的常数项为k,则直线y=kx与曲线y=x2围成的封闭图形的面积为( )
| 1 |
| x |
| A.3 | B.
| C.9 | D.
|
设(
+x2)3的展开式的通项公式为 Tr+1=
•xr-3•x2r=
•x3r-3,
令3r-3=0,r=1,故展开式的常数项为k=3.
则直线y=kx即y=3x,由
,求得直线y=kx与曲线y=x2围成交点坐标为(0,0)、(3,9),
故直线y=kx与曲线y=x2围成图形的面积为
(3x-x2)dx=(
x2-
)
=
,
故选:B.
| 1 |
| x |
| C | r3 |
| C | r3 |
令3r-3=0,r=1,故展开式的常数项为k=3.
则直线y=kx即y=3x,由
|
故直线y=kx与曲线y=x2围成图形的面积为
| ∫ | 30 |
| 3 |
| 2 |
| x3 |
| 3 |
| | | 30 |
| 9 |
| 2 |
故选:B.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目


 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.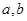 的值;
的值; :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率 ;(3)求
;(3)求 .
. (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P( <X<
<X< )的值为( )
)的值为( )