题目内容
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列.
(1)0.5(2)0.8(3)
| ξ | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.096 | 0.384 | 0.512 |
解:记A表示事件:进入商场的1位顾客购买甲种商品;记B表示事件:进入商场的1位顾客购买乙种商品;记C表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种;记D表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种.
(1)C=A·B+A·B,
P(C)=P(A·B+A·B)=P(A·B)+P(A·B)=P(A)·P(B)+P(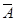 )·P(B)=0.5×0.4+0.5×0.6=0.5.
)·P(B)=0.5×0.4+0.5×0.6=0.5.
(2)D=A·B,
P(D)=P(A·B)=P(A)·P(B)=0.5×0.4=0.2,
P(D)=1-P(D)=0.8.
(3)ξ~B(3,0.8),故ξ的分布列
P(ξ=0)=0.23=0.008;
P(ξ=1)=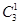 ×0.8×0.22=0.096;
×0.8×0.22=0.096;
P(ξ=2)=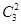 ×0.82×0.2=0.384;
×0.82×0.2=0.384;
P(ξ=3)=0.83=0.512.
(1)C=A·B+A·B,
P(C)=P(A·B+A·B)=P(A·B)+P(A·B)=P(A)·P(B)+P(
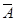 )·P(B)=0.5×0.4+0.5×0.6=0.5.
)·P(B)=0.5×0.4+0.5×0.6=0.5.(2)D=A·B,
P(D)=P(A·B)=P(A)·P(B)=0.5×0.4=0.2,
P(D)=1-P(D)=0.8.
(3)ξ~B(3,0.8),故ξ的分布列
P(ξ=0)=0.23=0.008;
P(ξ=1)=
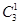 ×0.8×0.22=0.096;
×0.8×0.22=0.096;P(ξ=2)=
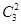 ×0.82×0.2=0.384;
×0.82×0.2=0.384;P(ξ=3)=0.83=0.512.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.096 | 0.384 | 0.512 |

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率;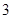 次,每次相互独立;
次,每次相互独立;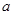 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为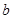 ,已知
,已知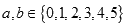 ,若
,若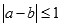 ,则本次竞猜成功;
,则本次竞猜成功;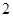 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.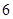 人组成的代表队中选
人组成的代表队中选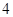 人参加此游戏,这
人参加此游戏,这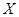 ,求
,求
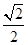 C.1-
C.1-