题目内容
【题目】已知等差数列{an}的各项均为正数，a1＝1，前n项和为Sn.数列{bn}为等比数列，b1＝1，且b2S2＝6，b2＋S3＝8.
(1)求数列{an}与{bn}的通项公式；
(2)求
.
【答案】（1）an＝n，bn＝2n－1（2）
【解析】试题分析：（1）设等差数列{an}的公差为d，d＞0，{bn}的公比为q，运用等差数列和等比数列的通项公式和求和公式，解方程可得公差和公比，即可得到所求通项公式；
（2）明确通项
的表达式，利用错位相减法求和.
试题解析：
(1)设等差数列{an}的公差为d，d>0，等比数列{bn}的公比为q，
则an＝1＋(n－1)d，bn＝qn－1.
依题意有
解得
或
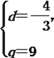(舍去)．
故an＝n，bn＝2n－1.
(2)由(1)知Sn＝1＋2＋…＋n＝
n(n＋1)，
即
＝
＝2
，
故
＋
＋…＋＝2
＝2
＝
.
练习册系列答案
相关题目
