题目内容
9.若a+b=1,则恒有( )| A. | ab≥$\frac{1}{4}$ | B. | ab≤$\frac{1}{4}$ | C. | $\frac{1}{ab}$≥4 | D. | a2+b2≥1 |
分析 取特值可排除A、C、D,由基本不等式求最值和分类讨论的方法可证B正确.
解答 解:取a=-2,b=3,ab=-6,显然A、C错误;
再取a=b=$\frac{1}{2}$,a2+b2=$\frac{1}{2}$,选项D错误;
对于选项B,当ab均为正数时,由基本不等式可得ab≤($\frac{a+b}{2}$)2=$\frac{1}{4}$,
当且仅当a=b=$\frac{1}{2}$时取等号,当ab一正一负时,显然成立;
当ab有一个为0时,也成了,ab不会同为负数,故恒成立.
故选:B.
点评 本题考查基本不等式求最值,取特值验证是解决问题的关键,属基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
4.|z-5+12i|≤2,则|z|的最小值为( )
| A. | 7 | B. | 9 | C. | 11 | D. | 15 |
14.在△ABC中,若a=7,b=8,c=3,则最大角的余弦是( )
| A. | $-\frac{1}{5}$ | B. | $-\frac{1}{6}$ | C. | $-\frac{1}{7}$ | D. | $-\frac{1}{8}$ |
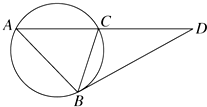 过D作圆的切线切于B点,作割线交圆于A、C两点,若BD=3,AD=4,AB=2,则BC=$\frac{3}{2}$.
过D作圆的切线切于B点,作割线交圆于A、C两点,若BD=3,AD=4,AB=2,则BC=$\frac{3}{2}$.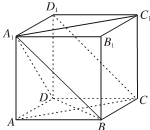 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.