题目内容
19．
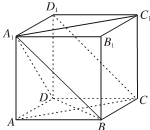已知正方体ABCD-A1B1C1D1．（1）求证：D1C∥平面A1BD．
（2）求异面直线A1D与D1C所成的角．
分析 （1）先根据A1D1∥BC且A1D1=BC，得到A1D1CB为平行四边形⇒A1B∥CD1，即可得到结论；
（2）利用线面、面面平行的判定定理得到∠BA1D是异面直线A1D与D1C所成的角．
解答 （1）证明：因为ABCD-A1B1C1D1是正方体，
所以A1D1∥BC，A1D1=BC；B1C1∥BC，B1C1=BC
所以A1D1∥BC，A1D1=BC，
所以四边形A1BCD1是平行四边形．
则A1B∥CD1．
又A1B?平面ABD1，CD1?面ABD1，
所以D1C∥平面A1BD．
（2）解：因为A1D1=BC且A1D1∥BC，
所以A1BCD1是平行四边形，
则D1C∥A1B，
所以∠BA1D是异面直线A1D与D1C所成的角，
因为A1D=D1C=BD，所以∠BA1D=60°．
点评 本题主要考查线面所成的角，线面平行以及面面垂直．是对立体几何知识的综合考查，属于综合题目．
练习册系列答案
名师导航单元期末冲刺100分系列答案
相关题目
9．若a+b=1，则恒有（ ）
| A． | ab≥$\frac{1}{4}$ | B． | ab≤$\frac{1}{4}$ | C． | $\frac{1}{ab}$≥4 | D． | a2+b2≥1 |
10．下列说法正确的是（ ）
| A． | 正切函数在定义域内为单调增函数 | |
| B． | 若α是第一象限角，则$\frac{α}{2}$是第一象限角 | |
| C． | 用秦九韶算法计算多项式f（x）=3x6+5x4+6x3-4x-5当x=3时的值时，v2=3v1+5=32 | |
| D． | 若扇形圆心角为2弧度，且扇形弧所对的弦长为2，则这个扇形的面积为$\frac{1}{{{{sin}^2}1}}$ |
14．$|\vec a|=1，|\vec b|=2$则$\vec a$与$\vec b$的夹角为120°，则$（\vec a+2\vec b）•（2\vec a+\vec b）$的值为（ ）
| A． | -5 | B． | 5 | C． | $-\sqrt{5}$ | D． | $\sqrt{5}$ |