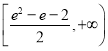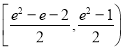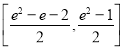题目内容
【题目】已知函数![]() (b为常数)
(b为常数)
(1)若b=1,求函数H(x)=f(x)﹣g(x)图象在x=1处的切线方程;
(2)若b≥2,对任意x1,x2∈[1,2],且x1≠x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求实数b的值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)将b=1代入,求导后得到斜率,求出切点,利用点斜式得到切线方程;
(2)分析可知,函数f(x)=lnx在区间[1,2]上是增函数,函数g(x)在区间[1,2]上是减函数,进而问题等价于f(x1)+g(x1)>f(x2)+g(x2),进一步等价于![]() 在区间[1,2]上恒成立,由此即可得解.
在区间[1,2]上恒成立,由此即可得解.
(1)若b=1,函数![]() ,
,
∴![]() ,故
,故![]() 又切点为
又切点为![]() ,
,
故所求切线方程为2x﹣2y﹣1=0;
(2)不妨设x1>x2,
∵函数f(x)=lnx在区间[1,2]上是增函数,
∴f(x1)>f(x2),
∵函数g(x)图象的对称轴为x=b,且b>2,
∴当b≥2时,函数g(x)在区间[1,2]上是减函数,
∴g(x1)<g(x2),
∴|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|等价于f(x1)+g(x1)>f(x2)+g(x2),
等价于函数![]() 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
等价于![]() 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
等价于![]() 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
∴b≤2,
又b≥2,故b=2.

练习册系列答案
相关题目