题目内容
【题目】若不等式![]() (
(![]() 为自然对数的底数)对
为自然对数的底数)对![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.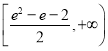 B.
B.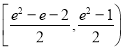 C.
C.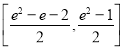 D.
D.![]()
【答案】A
【解析】
解法一利用函数的整体性,抓住关键点处的单调函数值不超过![]() ,解两个含绝对值不等式;解法二利用函数的整体性,求出
,解两个含绝对值不等式;解法二利用函数的整体性,求出![]() 的范围,再利用绝对值的基本解法,分离参变量;解析三对参数进行讨论,目的是寻找函数的最大值,由此求得
的范围,再利用绝对值的基本解法,分离参变量;解析三对参数进行讨论,目的是寻找函数的最大值,由此求得![]() 的取值范围..
的取值范围..
解法1:设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,所以
,所以![]() ,
,
为使不等式![]() 对
对![]() 成立,则
成立,则![]()
而![]() ,
,
所以![]() ,解得
,解得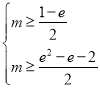
所以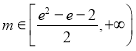 ,故选A.
,故选A.
解法2:设![]() ,则
,则![]()
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]()
为使不等式![]() 对
对![]() 成立
成立
即![]() 对
对![]() 成立
成立
所以![]() 对
对![]() 成立,即
成立,即![]()
所以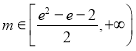 ,故选A.
,故选A.
解法3:设![]() ,则
,则![]()
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]()
为使不等式![]() 对
对![]() 成立
成立
即不等式![]() 对
对![]() 成立
成立
当![]() 时,
时,![]() 对
对![]() 成立,即
成立,即![]() ,不符
,不符
当![]() 时,
时,![]() 对
对![]() 成立,显然恒成立
成立,显然恒成立
当![]() 时,
时,![]()
只需![]() ,即
,即![]()
所以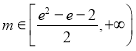 .
.
故选:A.

练习册系列答案
相关题目