题目内容
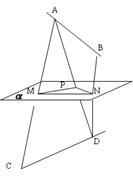
已知：a，b是两条异面直线，a^a，b^b，a∩b=
，AB是a，b公垂线，交a于A，交b于B
求证：AB∥
，AB是a，b公垂线，交a于A，交b于B求证：AB∥
证明见解析
证明方法一：（利用线面垂直的性质定理）
过A作
∥b，则a，可确定一平面γ
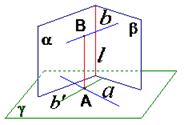∵AB是异面垂线的公垂线，
即AB^a，AB^b
∴AB^
∴AB^γ
∵a^α，b^β，a∩b=
∴
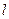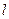^a，^b ∴^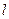
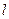∴^γ ∴AB∥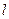
证明方法二：（利用同一平面内垂直于同一直线的两条直线互相平行）
∵AB是异面直线a，b的公垂线，过AB与a作平面γ，γ∩a=m
∵a^a ∴a^m
又a^AB，ABÌγ
∴m∥AB
又过AB作平面g，g∩β=n
同理：n∥AB
∴m∥n，于是有m∥β
又a∩b=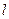 ∴m∥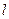
∴AB∥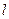
过A作
∥b，则a，可确定一平面γ∵AB是异面垂线的公垂线，即AB^a，AB^b
∴AB^
∴AB^γ
∵a^α，b^β，a∩b=
∴
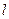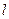^a，^b ∴^∴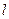
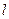^γ ∴AB∥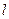证明方法二：（利用同一平面内垂直于同一直线的两条直线互相平行）
∵AB是异面直线a，b的公垂线，过AB与a作平面γ，γ∩a=m
∵a^a ∴a^m
又a^AB，ABÌγ
∴m∥AB
又过AB作平面g，g∩β=n
同理：n∥AB
∴m∥n，于是有m∥β
又a∩b=
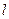∴m∥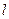∴AB∥
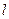
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
中，点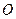
，
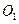分别是四边形
，
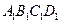的对角线的交点，点
，
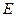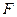分别是四边形
，
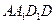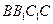的对角线的交点，点
，
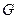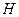分别是四边形
，
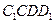的对角线的交点．求证：
．
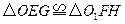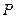为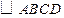
所在平面外一点，
，
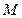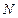分别是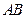
，
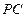的中点，平面
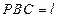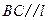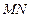平面
．
．
与平面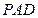
是否平行？试证明你的结论．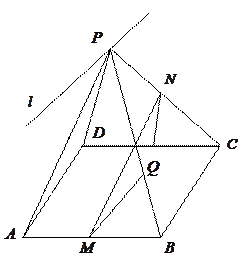
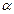，且AB、CD在
。
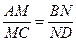中，E、F、G、H、M、N分别是正方体六个面的中心．求证：平面EFG//平面HMN.
中，
分别是
的中点．
平面
；（2）
平面
．
、
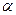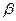，且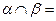
AB,PC⊥
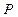
（2）若F为侧棱PA上的一点，且
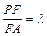， 则为何值时，PA平面BDF？ 并求此时几何体F—BDC的体积．
，
平面
，且
，
，
．