题目内容
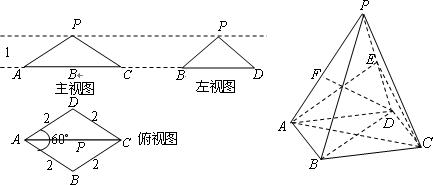
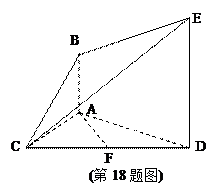
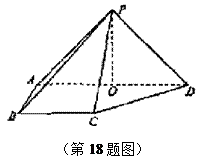
一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点.
(1)求证:PB//平面AEC;
 (2)若F为侧棱PA上的一点,且
(2)若F为侧棱PA上的一点,且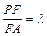 , 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.
, 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.
(1)求证:PB//平面AEC;
 (2)若F为侧棱PA上的一点,且
(2)若F为侧棱PA上的一点,且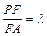 , 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.
, 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.
(2)
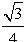
(1)由图形可知该四棱锥和底面ABCD是菱形,且有一角为,边长为2,
锥体高度为1。
设AC,BD和交点为O,连OE,OE为△DPB的中位线,
OE//PB, 3分
EO面EAC,PB面EAC内, PB//面AEC。 6分
(2)过O作OFPA垂足为F ,
在Rt△POA中,PO=1,AO=,PA=2,在Rt△POB中,PO=1,BO=1,PB=, 8分
过B作PA的垂线BF,垂足为F,连DF,由于△PAB≌△PAD,故DF⊥PA,DF∩BF=F,因此PA⊥面BDF. 10分
在等腰三角形PAB中解得AF=,进而得PF=" "
即当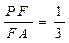 时,PA面BDF, 12分
时,PA面BDF, 12分
此时F到平面BDC的距离FH=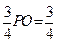
 14分
14分
锥体高度为1。
设AC,BD和交点为O,连OE,OE为△DPB的中位线,
OE//PB, 3分
EO面EAC,PB面EAC内, PB//面AEC。 6分
(2)过O作OFPA垂足为F ,
在Rt△POA中,PO=1,AO=,PA=2,在Rt△POB中,PO=1,BO=1,PB=, 8分
过B作PA的垂线BF,垂足为F,连DF,由于△PAB≌△PAD,故DF⊥PA,DF∩BF=F,因此PA⊥面BDF. 10分
在等腰三角形PAB中解得AF=,进而得PF=" "
即当
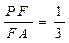 时,PA面BDF, 12分
时,PA面BDF, 12分此时F到平面BDC的距离FH=
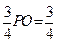
 14分
14分
练习册系列答案
相关题目
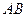
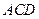
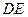
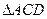
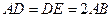 ,且
,且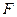 是
是 的中点.
的中点.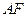 ∥平面
∥平面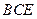 ;
;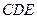 .
.
 ,AB是a,b公垂线,交a于A,交b于B
,AB是a,b公垂线,交a于A,交b于B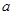 与平面
与平面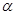 平行的条件是( ).
平行的条件是( ).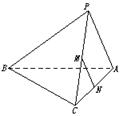
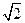 ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中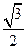 ?若存在,求出
?若存在,求出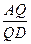 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.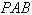 是否垂直于平面
是否垂直于平面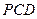 ?
?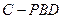 的体积.
的体积.

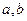 为直线,
为直线,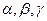 为平面,有下列三个命题:
为平面,有下列三个命题: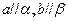 ,则
,则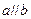 ;
;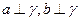 ,则
,则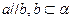 ,则
,则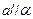 ;
;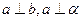 ,则
,则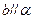 ;
;