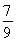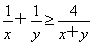题目内容
已知平面向量a=(1,x),b=(2x+3,-x),x∈R.
(1)若a⊥b,求x的值;
(2)若a∥b,求|a-b|的值.
(1)x=-1或x=3(2)2或2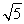 .
.
【解析】(1)若a⊥b,
则a·b=(1,x)·(2x+3,-x)=1×(2x+3)+x(-x)=0,
整理得x2-2x-3=0,解得x=-1或x=3.
(2)若a∥b,则有1×(-x)-x(2x+3)=0,
即x(2x+4)=0,解得x=0或x=-2.
当x=0时,a=(1,0),b=(3,0),a-b=(-2,0),
∴|a-b|=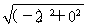 =2;
=2;
当x=-2时,a=(1,-2),b=(-1,2),a-b=(2,-4),
∴|a-b|=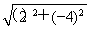 =2
=2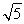 .
.
综上,可知|a-b|=2或2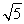 .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目