题目内容
设两向量e1、e2满足|e1|＝2，|e2|＝1，e1、e2的夹角为60°，若向量2te1＋7e2与向量e1＋te2的夹角为钝角，求实数t的取值范围．
∪
【解析】由已知得
＝4，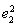
＝1，e1·e2＝2×1×cos60°＝1.
∴(2te1＋7e2)·(e1＋te2)＝2t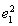
＋(2t2＋7)e1·e2＋7t
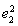＝2t2＋15t＋7.欲使夹角为钝角，需2t2＋15t＋7＜0，得－7＜t＜－
.
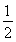设2te1＋7e2＝λ(e1＋te2)(λ＜0)，
∴
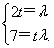，∴2t2＝7，
∴t＝－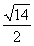
，此时λ＝－
.
即t＝－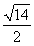
时，向量2te1＋7e2与e1＋te2的夹角为π.
∴夹角为钝角时，t的取值范围是∪
练习册系列答案
相关题目
