题目内容
9.在Rt△ABC中有这样一个结论:$\overrightarrow{BA}$•$\overrightarrow{BC}$=|$\overrightarrow{BC}$|2.利用这一结论求解:如图,在?ABCD中,AP⊥BD,垂足为P,$\overrightarrow{AP}$•$\overrightarrow{AC}$=8,则AP=2.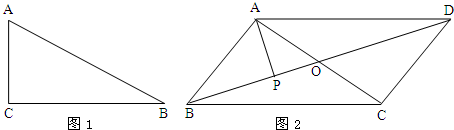
分析 通过建立$\overrightarrow{AP}$•$\overrightarrow{AO}$与$\overrightarrow{AP}$•$\overrightarrow{AC}$之间的关系,利用Rt△ABC中已知结论计算即得结论.
解答 解:由题意可知$\overrightarrow{AP}$•$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AP}$•$\overrightarrow{AC}$=$\frac{1}{2}$•8=4,
∴AP=$\sqrt{|\overrightarrow{AP}{|}^{2}}$=$\sqrt{\overrightarrow{AP}•\overrightarrow{AO}}$=$\sqrt{4}$=2,
故答案为:2.
点评 本题考查平面向量数量积的运算,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列说法中正确的是( )
| A. | 若命题p:?x∈R有x2>0,则¬p:?x∈R有x2≤0 | |
| B. | 若p是q的充分不必要条件,则¬p是¬q的必要不充分条件 | |
| C. | 若命题p:$\frac{1}{x-1}$>0,则¬p:$\frac{1}{x-1}$≤0 | |
| D. | 方程ax2+x+a=0有唯一解的充要条件是a=±$\frac{1}{2}$ |
 在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,点M是棱PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,点M是棱PA的中点.