题目内容
20.在直角坐标系xoy中,曲线C1的参数方程为$\left\{{\begin{array}{l}{x=2-\sqrt{2}t}\\{y=-1+\sqrt{2}t}\end{array}}\right.$(t为参数),以原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为$ρ=\frac{2}{{\sqrt{1+3{{sin}^2}θ}}}$(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设点M(2,-1),曲线C1与曲线C2交于A,B,求|MA|•|MB|的值.
分析 (1)曲线C1的参数方程为$\left\{{\begin{array}{l}{x=2-\sqrt{2}t}\\{y=-1+\sqrt{2}t}\end{array}}\right.$(t为参数),两式相加消去参数t即可化为普通方程;由曲线C2的极坐标方程为$ρ=\frac{2}{{\sqrt{1+3{{sin}^2}θ}}}$,平方化为ρ2+3ρ2sin2θ=4,利用$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{y=ρsinθ}\end{array}\right.$即可化为直角坐标方程.(2)将$\left\{\begin{array}{l}x=2-\frac{{\sqrt{2}}}{2}t\\ y=-1+\frac{{\sqrt{2}}}{2}t\end{array}\right.({t为参数})$代入C2直角坐标方程得$5{t^2}-12\sqrt{2}t+8=0$,利用MA|•|MB|=t1•t2即可得出.
解答 解:(1)曲线C1的参数方程为$\left\{{\begin{array}{l}{x=2-\sqrt{2}t}\\{y=-1+\sqrt{2}t}\end{array}}\right.$(t为参数),消去参数t化为x+y=1;
由曲线C2的极坐标方程为$ρ=\frac{2}{{\sqrt{1+3{{sin}^2}θ}}}$,平方化为ρ2+3ρ2sin2θ=4,∴x2+4y2=4,化为直角坐标方程:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)将$\left\{\begin{array}{l}x=2-\frac{{\sqrt{2}}}{2}t\\ y=-1+\frac{{\sqrt{2}}}{2}t\end{array}\right.({t为参数})$代入C2直角坐标方程得$5{t^2}-12\sqrt{2}t+8=0$,
∴${t_1}•{t_2}=\frac{8}{5}$,
∴MA|•|MB|=${t_1}•{t_2}=\frac{8}{5}$.
点评 本题考查了参数方程化为直角坐标方程、极坐标方程与直角坐标方程的互化、直线参数方程的应用,考查了推理能力与计算能力,属于中档题.

| A. | M1=M2=M3=M4 | B. | M1?M2?M3?M4 | C. | M1⊆M2⊆M3⊆M4 | D. | M1?M2,M2=M3⊆M4 |
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 不是对称图形 |
| A. | 函数f(x)在(0,+∞)上是增函数 | B. | 函数f(x)在(0,+∞)上是减函数 | ||
| C. | 函数f(x)是奇函数 | D. | 函数f(x)是偶函数 |
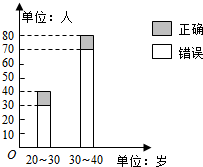 “开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考)
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d)
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |