题目内容
4．已知tan（α+β）=$\frac{2}{5}$，tan（β-$\frac{π}{4}$）=$\frac{1}{4}$，则tanα=-$\frac{19}{25}$．分析 由条件利用两角和差的正切公式求得tanβ的值，可得tanα=tan[（α+β）-β]的值．
解答 解：∵tan（β-$\frac{π}{4}$）=$\frac{tanβ-1}{1+tanβ}$=$\frac{1}{4}$，∴tanβ=$\frac{5}{3}$，
又tan（α+β）=$\frac{2}{5}$，∴tanα=tan[（α+β）-β]=$\frac{tan（α+β）-tanβ}{1+tan（α+β）tanβ}$=$\frac{\frac{2}{5}-\frac{5}{3}}{1+\frac{2}{5}×\frac{5}{3}}$=-$\frac{19}{25}$，
故答案为：-$\frac{19}{25}$．
点评 本题主要考查两角和差的正切公式的应用，属于基础题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
14．将2n按如表的规律填在5列的数表中，设22015排在数表的第n行，第m列，则m+n=506
| 21 | 22 | 23 | 24 | |
| 28 | 27 | 26 | 25 | |
| 29 | 210 | 211 | 212 | |
| 216 | 215 | 214 | 213 | |
| … | … | … | … | … |
15．
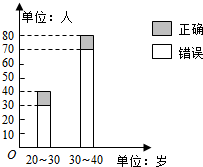“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
（2）现计划在这次场外调查中按年龄段选取9名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．（1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
12．若双曲线t2y2-x2=t2（t≠0）经过点$（2，\sqrt{2}）$，则该双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
19．在等腰△ABC中，角A，B，C的对边分别为a，b，c，若sinB=sinAcosC-$\frac{1}{2}$sinC，且a=$\sqrt{3}$，则△ABC的面积为（ ）
| A． | $\frac{3\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{4}$ | ||
| C． | $\sqrt{3}$ | D． | 条件不足，无法计算 |
16．已知函数f（x）满足f（0）=1，且对于任意实数x，y∈R都有：f（xy+1）=f（x）f（y）-f（y）-x+2，若x∈[1，3]，则$\frac{f（x-1）}{{f}^{2}（x）+1}$的最大值为（ ）
| A． | $\frac{\sqrt{2}-1}{2}$ | B． | $\frac{\sqrt{2}+1}{2}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{17}$ |
13．已知M={x|x2-x=0}，N={y|y2+y=0}，则M∩N=（ ）
| A． | {-1，1，0} | B． | {-1，1} | C． | {0} | D． | ∅ |