题目内容
1.在直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$(φ为参数,0≤φ≤π).以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C与θ=$\frac{π}{3}$(ρ>0)所表示的图形的交点的直角坐标是$(\frac{1}{2},\frac{\sqrt{3}}{2})$.分析 曲线C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$(φ为参数,0≤φ≤π),化为直角坐标方程,再化为极坐标方程ρ=2cosθ$(θ∈[0,\frac{π}{2}])$,联立$\left\{\begin{array}{l}{θ=\frac{π}{3}}\\{ρ=2cosθ}\end{array}\right.$,解得即可得出.
解答 解:曲线C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$(φ为参数,0≤φ≤π),化为(x-1)2+y2=1,(y≥0),
化为极坐标ρ2-2ρcosθ=0,即ρ=2cosθ$(θ∈[0,\frac{π}{2}])$,
联立$\left\{\begin{array}{l}{θ=\frac{π}{3}}\\{ρ=2cosθ}\end{array}\right.$,解得$θ=\frac{π}{3}$,ρ=1,
∴两图形的交点直角坐标为:$(\frac{1}{2},\frac{\sqrt{3}}{2})$.
故答案为:$(\frac{1}{2},\frac{\sqrt{3}}{2})$.
点评 本题考查了参数方程化为直角坐标方程、极坐标方程与直角坐标方程的互化,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.当-$\frac{π}{2}$<x<$\frac{π}{2}$时,函数y=lg|x|的图象是( )
| A. | 关于原点对称 | B. | 关于x轴对称 | C. | 关于y轴对称 | D. | 不是对称图形 |
12.若双曲线t2y2-x2=t2(t≠0)经过点$(2,\sqrt{2})$,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
16.已知函数f(x)满足f(0)=1,且对于任意实数x,y∈R都有:f(xy+1)=f(x)f(y)-f(y)-x+2,若x∈[1,3],则$\frac{f(x-1)}{{f}^{2}(x)+1}$的最大值为( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{17}$ |
13.已知M={x|x2-x=0},N={y|y2+y=0},则M∩N=( )
| A. | {-1,1,0} | B. | {-1,1} | C. | {0} | D. | ∅ |
11.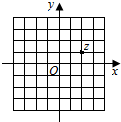 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |