题目内容
（本小题满分12分)
已知点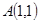
是椭圆
上一点，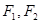
是椭圆的两焦点，且满足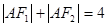
(Ⅰ) 求椭圆的两焦点坐标；
(Ⅱ) 设点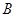
是椭圆上任意一点，如果
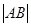最大时，求证
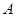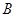、两点关于原点
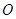不对称.
已知点
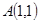是椭圆上一点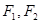，是椭圆的两焦点，且满足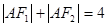(Ⅰ) 求椭圆的两焦点坐标；
(Ⅱ) 设点
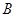是椭圆上任意一点，如果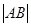最大时，求证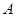、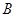两点关于原点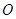不对称.解：
（I）由椭圆定义知：
∴
∴ 
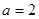把
代入得
∴ 
则椭圆方程为
∴ 
∴ 
故两焦点坐标为
．…………6分
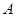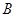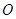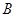（II）用反证法 ： 假设、两点关于原点对称，则点坐标为
，
此时
取椭圆上一点
，则
∴ 
．
从而此时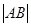不是最大，这与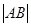最大矛盾，所以命题成立．…………12分
（I）由椭圆定义知：
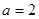∴ ∴ 把代入得∴ 则椭圆方程为
∴ ∴ 故两焦点坐标为
．…………6分（II）用反证法 ： 假设
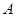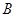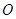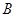、两点关于原点对称，则点坐标为，此时
取椭圆上一点，则 ∴ ．从而此时
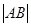不是最大，这与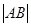最大矛盾，所以命题成立．…………12分略
练习册系列答案
相关题目
（
），
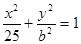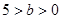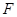为椭圆右焦点，
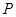为椭圆在短轴上的一个顶点，
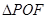的面积为6,（
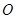为坐标原点）；
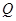，使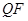
的中垂线过点
的左焦点
是长轴的一个四等分点，点A、B分别为椭圆的左、右顶点，过点F且不与y轴垂直的直线
交椭圆于C、D两点，记直线AD、BC的斜率分别为
轴时，求
的值；
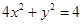上，则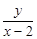
的最小值为（ ）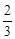
经过点
，对称轴为坐标轴，焦点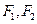
在
轴上，离心率
，
＋
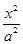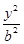＝1(a>b>0)的左焦点为F，右顶点为A，点B在椭圆上，且BF⊥x轴，直线AB交y轴于点P.若
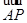＝2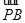
，则椭圆的离心率是（ ）
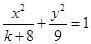的离心率为
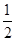，则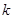
的值为 ____________
的左右焦点为
;直线
经过
交椭圆于
两点.
的周长为定值.
的左、右焦点分别是F1，F2，过F2作倾斜角为
的直线与椭圆的一个交点为M，若MF1垂直于x轴，则椭圆的离心率为______