题目内容
【题目】在正四面体ABCD中，M，N分别是BC和DA的中点，则异面直线MN和CD所成角为 ．
【答案】
【解析】解：如图，取AC中点O，连结AM、DM、OM、ON，
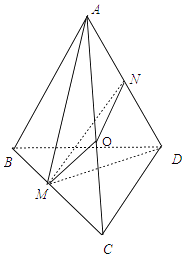
设正四面体ABCD的棱长为2，
∵M，N分别是BC和DA的中点，
∴AM=DM= 
，MN= 
，
MN 
=1，NO 
=1，
∴∠MNO是异面直线MN和CD所成角（或所成角的补角），
cos∠MNO= 
= 
= 
，
∴∠MNO= ．
∴异面直线MN和CD所成角为 ．
所以答案是： ．
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限x和支出的维修费用y（万元），有如下表的统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系，试求：
（1）线性回归方程 
.
（2）估计使用年限为10年时，维修费用是多少.
（3）计算总偏差平方和、残差平方和及回归平方和.
（4）求 
并说明模型的拟合效果.
