题目内容
【题目】(2015·江苏)已知集合X={1,2,3},Yn={1,2,3...,n}(n![]() N*),Sn={(a,b)|a整除b或b整除a, a
N*),Sn={(a,b)|a整除b或b整除a, a![]() X, b
X, b![]() Yn}, 令f(n)表示集合Sn所包含元素的个数。
Yn}, 令f(n)表示集合Sn所包含元素的个数。
(1)写出f(6)的值;
(2)当n≥6时,写出f(n)的表达式,并用数学归纳法证明.
【答案】
(1)
13
(2)
f(n)=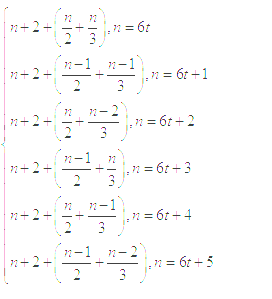
【解析】
(1) 根据题意按a分类计数,a=1, b=1,2,3,4,5,6, a=2, b=1,2,4,5, a=3,b=1,3,6 共13个(2)由(1)知a=1, b=1,2,3,...,n, a=2, b=1,2,4,....,2k, a=3,b=1,3,...,3k(k![]() N*), ,所以当n≥6时,f(n)的表达方式要按2x3=6除的余数进行分类,最后不难利用数学归纳法进行证明。
N*), ,所以当n≥6时,f(n)的表达方式要按2x3=6除的余数进行分类,最后不难利用数学归纳法进行证明。
(1)f(6)=13, (2)当n≥6时, f(n)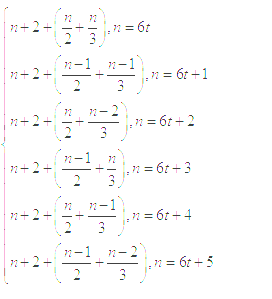 (t
(t![]() N*).
N*).
下面用数学归纳法证明:①n=6时,f(6)=6+2+![]() =13, 结论成立。
=13, 结论成立。
②假设n=k(k≥6)时结论成立,那么n=k+1时,Sk+1在Sk的基础上新增的元素在(1,k+1), (2, k+1), (3, k+1)中产生,分以下情形讨论。
1)若k+1=6t, 则k=6(t-1)+5, 此时有f(k+1)=f(k)+3=k+2+![]() +
+![]() +3=(k+1)+2+
+3=(k+1)+2+![]() +
+![]() , 结论成立。
, 结论成立。
2)若k+1=6t+1, 则k=6t, 此时有f(k+1)=f(k)+1=k+2+![]() +
+![]() +1=(k+1)+2+
+1=(k+1)+2+![]() +
+![]() , 结论成立。
, 结论成立。
3)若k+1=6t+1, 则k=6t+1, 此时有f(k+1)=f(k)+2=k+2+![]() +
+![]() +2=(k+1)+2+
+2=(k+1)+2+![]() +
+![]() , 结论成立。
, 结论成立。
4)若k+1=6t+3, 则k=6t+2, 此时有f(k+1)=f(k)+2=k+2+![]() +
+![]() +2=(k+1)+2+
+2=(k+1)+2+![]() +
+![]() , 结论成立。
, 结论成立。
5)若k+1=6t+4, 则k=6t+3, 此时有f(k+1)=f(k)+2=k+2+![]() +
+![]() +2=(k+1)+2+
+2=(k+1)+2+![]() +
+![]() , 结论成立。
, 结论成立。
5)若k+1=6t+5, 则k=6t+5, 此时有f(k+1)=f(k)+2=k+2+![]() +
+![]() +1=(k+1)+2+
+1=(k+1)+2+![]() +
+![]() , 结论成立。
, 结论成立。
综上所述, 结论对满足n≥6的自然数n 均成立。
【考点精析】认真审题,首先需要了解数学归纳法的定义(数学归纳法是证明关于正整数n的命题的一种方法).
