题目内容
4.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且过点($\frac{1}{2}$,$\frac{\sqrt{14}}{4}$).(1)求椭圆C的标准方程;
(2)设F是椭圆C的左焦点,过点P(-2,0)的直线交椭圆于A,B两点,求△ABF面积的最大值.
分析 (1)利用椭圆的性质求得椭圆方程
(2)直线AB的方程为y=k(x+2)(k≠0)设点AA(x1,y1)B(x2,y2),联立消去y得(1+2k2)x2+8k2x+8k2-2=0,由弦长公式求得底边边长,由点到直线距离求得高,继而求得面积.
解答 解:(1)因为椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率为$\frac{\sqrt{2}}{2}$,所以$\frac{c}{a}=\frac{\sqrt{2}}{2}$.
又椭圆C过点($\frac{1}{2},\frac{\sqrt{14}}{4}$),所以$\frac{1}{4{a}^{2}}+\frac{7}{8{b}^{2}}=1$.
同时结合a2=b2+c2,解得$a=\sqrt{2},b=1,c=1$所以椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$
(2)由题知:F(-1,0),显然直线AB的斜率存在,设为k,
则直线AB的方程为y=k(x+2)(k≠0),设点AA(x1,y1)B(x2,y2),联立消去y得(1+2k2)x2+8k2x+8k2-2=0
故△=(8k2)2-4(1+2k2)(8k2-2)
=8(1-k2)>0,所以$0<{k}^{2}<\frac{1}{2}$且${x}_{1}+{x}_{2}=-\frac{8{k}^{2}}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{8{k}^{2}-2}{1+2{k}^{2}}$
所以|AB|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1+}{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{\frac{8(1-2{k}^{2})}{(1+2{k}^{2})}}$.
点F到直线AB的距离为$d=\frac{|k|}{\sqrt{1+{k}^{2}}}$,所以${S}_{△AEF}=\frac{1}{2}×\frac{|k|}{\sqrt{1+{k}^{2}}}\sqrt{1+{k}^{2}}\sqrt{\frac{8(1-2{k}^{2})}{(1-2{k}^{2})^{2}}}$
=$\sqrt{2}\sqrt{\frac{-2{k}^{4}+{k}^{2}}{4{k}^{4}+4{k}^{2}+1}}$=$\sqrt{2}\sqrt{-\frac{1}{2}+\frac{1}{2}×\frac{6{k}^{2}+1}{4{k}^{4}+4{k}^{2}+1}}$令t=6k2+1∈(1,4)则${k}^{2}=\frac{t-1}{6}$
所以${S}_{△ABF}=\sqrt{2}\sqrt{-\frac{1}{2}+\frac{9}{2}×\frac{t}{{t}^{2}+4t+4}}$S=$\sqrt{2}\sqrt{-\frac{1}{2}+\frac{9}{2}×\frac{1}{t+\frac{4}{t}+4}}≤$
$\sqrt{2}\sqrt{-\frac{1}{2}+\frac{9}{2}×\frac{1}{4+4}}=\frac{\sqrt{2}}{4}$,
当且仅当$t=\frac{4}{t}$时,即t=2,k=$±\frac{\sqrt{6}}{6}$时,取等号,所以△ABF面积的最大值为$\frac{\sqrt{2}}{4}$.
点评 本题主要考查椭圆方程的求法和直线和圆锥曲线的综合问题,属于中档题型,高中经常涉及.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | a<1 | B. | a>1 | C. | a<2 | D. | a>2 |
| A. | -10 | B. | -8 | C. | -6 | D. | -4 |
从甲、乙两个分厂生产的零件中各抽出500件,量其内径尺寸的结果如下表:
甲厂的零件内径尺寸:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 15 | 30 | 125 | 198 | 77 | 35 | 20 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) | ||||
| 频数 | 40 | 70 | 79 | 162 | 59 | 55 | 35 | ||||
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.025 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
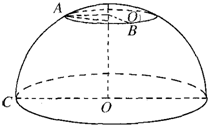 如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.