题目内容
(本小题满分12分)
已知三棱柱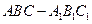 的侧棱垂直于底面,
的侧棱垂直于底面,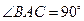 ,
,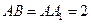 ,
,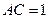 ,
,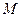 ,
,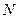 分别是
分别是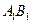 ,
,
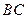 的中点.
的中点.
(1)证明: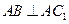 ;
;
(2)证明: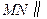 平面
平面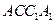 ;
;
(3)求二面角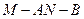 的余弦值.
的余弦值.
已知三棱柱
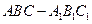 的侧棱垂直于底面,
的侧棱垂直于底面,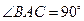 ,
,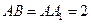 ,
,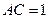 ,
,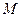 ,
,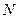 分别是
分别是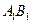 ,
,
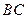 的中点.
的中点.(1)证明:
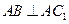 ;
;(2)证明:
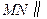 平面
平面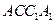 ;
;(3)求二面角
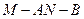 的余弦值.
的余弦值.
略
解法一:


(Ⅰ)证明:因为
 平面
平面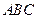 ,
,
所以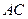 是
是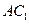 在平面
在平面 内的射影,… 2 分
内的射影,… 2 分
由条件可知
 ,
,
所以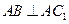 . ………………… 4 分
. ………………… 4 分
(Ⅱ)证明:设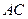 的中点为
的中点为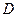 ,
,
连接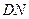 ,
,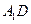 .
.
因为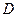 ,
,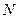 分别是
分别是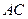 ,
,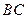 的中点,
的中点,
所以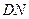
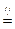
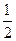
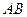 .
.
又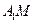 =
=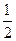
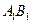 ,
,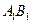
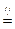
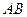 ,
,
所以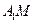
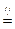
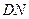 .
.
所以四边形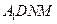 是平行四边形.
是平行四边形.
所以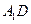
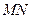 . …………………6 分
. …………………6 分
因为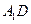
 平面
平面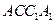 ,
,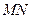
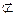 平面
平面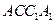 ,
,
所以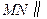 平面
平面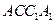 . …………… 8 分
. …………… 8 分
(Ⅲ)如图,设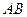 的中点为
的中点为
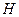 ,连接
,连接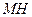 ,
,
所以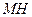
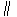
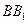 .
.
因为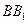
 底面
底面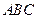 ,
,
所以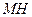
 底面
底面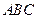 .
.
在平面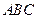 内,过点
内,过点 做
做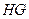
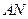 ,垂足为
,垂足为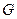 .
.
连接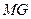 ,则
,则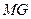
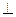
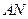 .
.
所以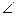
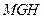 是二面角
是二面角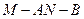 的平面角. ………………… 10 分
的平面角. ………………… 10 分
因为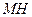 =
=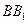 =2,
=2,
由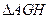 ∽
∽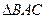 ,得
,得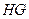 =
=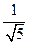 .
.
所以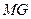 =
=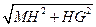 =
=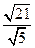 .
.
所以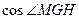 =
=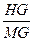 =
= .
.
二面角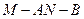 的余弦值是
的余弦值是 . ………………… 12 分
. ………………… 12 分
解法二:
依条件可知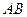 ,
,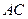 ,
,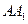 两两垂直.
两两垂直.
如图,以点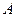 为原点建立空间直角坐标系
为原点建立空间直角坐标系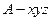 .
.
根据条件容易求出如下各点坐标:
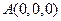 ,
,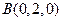 ,
,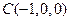 ,
,
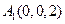 ,
, ,
,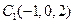 ,
,
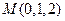 ,
,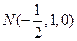 .
.
(Ⅰ)证明:因为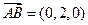 ,
,
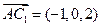 ,
,
所以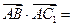
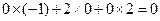 . ………………… 2
. ………………… 2 分
分
所以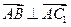 .
.
即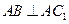 . ………………… 4 分
. ………………… 4 分
(Ⅱ)证明:因为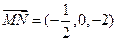 ,
,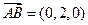 是平面
是平面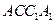 的一个法向量,
的一个法向量,
且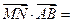
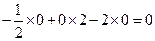 ,所以
,所以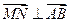 . ………6 分
. ………6 分
又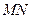
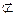 平面
平面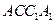 ,
,
所以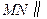 平面
平面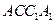 . ………………… 8 分
. ………………… 8 分
(Ⅲ)设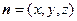 是平面
是平面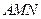 的法向量,
的法向量,
因为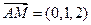 ,
,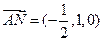 ,
,
由 得
得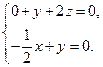 解得平面
解得平面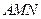 的一个法向量
的一个法向量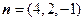 .
.
由已知,平面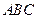 的一个法向量为
的一个法向量为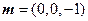 . ………………… 10 分
. ………………… 10 分
设二面角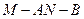 的大小为
的大小为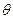 , 则
, 则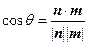 =
=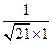 =
= .
.
二面角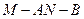 的余弦值是
的余弦值是 . ………………… 12 分
. ………………… 12 分


(Ⅰ)证明:因为

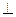 平面
平面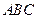 ,
,所以
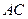 是
是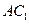 在平面
在平面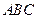 内的射影,… 2 分
内的射影,… 2 分由条件可知
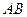
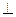
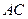 ,
,所以
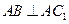 . ………………… 4 分
. ………………… 4 分(Ⅱ)证明:设
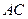 的中点为
的中点为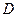 ,
,连接
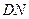 ,
,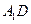 .
.因为
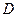 ,
,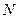 分别是
分别是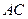 ,
,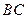 的中点,
的中点,所以
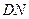
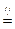
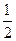
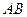 .
.又
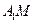 =
=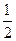
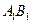 ,
,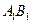
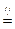
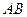 ,
,所以
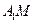
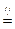
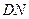 .
.所以四边形
 是平行四边形.
是平行四边形.所以
 . …………………6 分
. …………………6 分因为
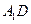
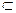 平面
平面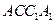 ,
,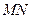
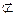 平面
平面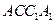 ,
,所以
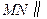 平面
平面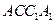 . …………… 8 分
. …………… 8 分(Ⅲ)如图,设
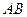 的中点为
的中点为
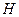 ,连接
,连接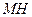 ,
,所以
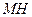
 .
.因为
 底面
底面 ,
,所以
 底面
底面 .
.在平面
 内,过点
内,过点 做
做
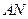 ,垂足为
,垂足为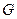 .
.连接
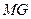 ,则
,则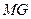
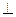
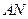 .
.所以
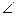
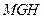 是二面角
是二面角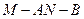 的平面角. ………………… 10 分
的平面角. ………………… 10 分因为
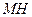 =
=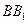 =2,
=2,由
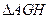 ∽
∽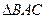 ,得
,得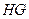 =
=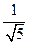 .
.所以
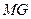 =
=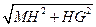 =
=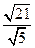 .
.所以
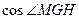 =
=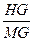 =
= .
.二面角
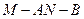 的余弦值是
的余弦值是 . ………………… 12 分
. ………………… 12 分解法二:
依条件可知
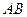 ,
,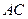 ,
,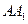 两两垂直.
两两垂直.如图,以点
 为原点建立空间直角坐标系
为原点建立空间直角坐标系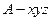 .
.根据条件容易求出如下各点坐标:
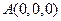 ,
,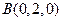 ,
,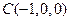 ,
,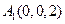 ,
, ,
,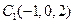 ,
,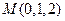 ,
,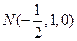 .
.(Ⅰ)证明:因为
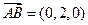 ,
,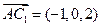 ,
,所以
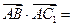
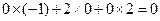 . ………………… 2
. ………………… 2 分
分所以
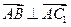 .
.即
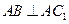 . ………………… 4 分
. ………………… 4 分(Ⅱ)证明:因为
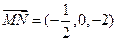 ,
,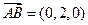 是平面
是平面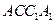 的一个法向量,
的一个法向量,且
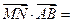
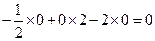 ,所以
,所以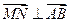 . ………6 分
. ………6 分又
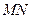
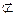 平面
平面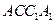 ,
,所以
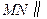 平面
平面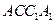 . ………………… 8 分
. ………………… 8 分(Ⅲ)设
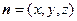 是平面
是平面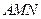 的法向量,
的法向量,因为
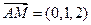 ,
,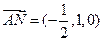 ,
,由
 得
得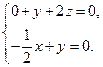 解得平面
解得平面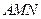 的一个法向量
的一个法向量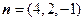 .
.由已知,平面
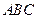 的一个法向量为
的一个法向量为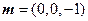 . ………………… 10 分
. ………………… 10 分设二面角
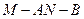 的大小为
的大小为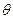 , 则
, 则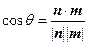 =
=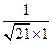 =
= .
.二面角
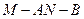 的余弦值是
的余弦值是 . ………………… 12 分
. ………………… 12 分
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
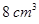 的正方体的顶点都在球面上,则球的体积是( )
的正方体的顶点都在球面上,则球的体积是( )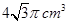
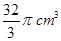
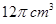
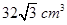
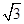 ,侧棱与底面所成角为600,则棱锥的体积为( )
,侧棱与底面所成角为600,则棱锥的体积为( ) 中,底面
中,底面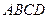 是
是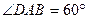 的菱形,
的菱形,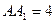 ,
,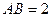 ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱 的中点.
的中点.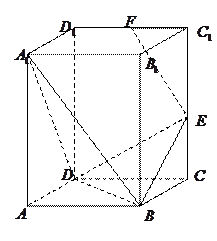
 ;
;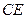 的长度,使得
的长度,使得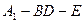 为直二面角.
为直二面角.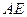 ;
;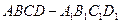 中,棱长为
中,棱长为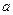
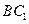 与
与 所成的角;
所成的角;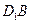 与平面
与平面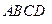 所成角的正切值;
所成角的正切值;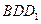
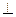 平面
平面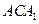 .
.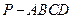 的底面为直角梯形,
的底面为直角梯形, ,
,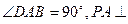 底面
底面 ,且
,且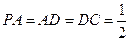 ,
, ,
, 是
是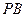 的中点。
的中点。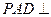 面
面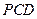 ;
;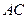 与
与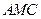 与面
与面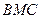 所成二面角的余弦值.
所成二面角的余弦值.
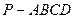 中,
中,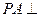 底面
底面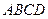 ,
,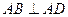 ,
,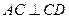 ,
,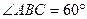 ,
,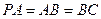 ,
,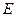 是
是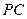 的中点.
的中点.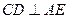 ;
;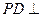 面
面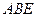 ;
;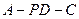 的平面角的正弦值.
的平面角的正弦值.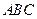 的边长为4,
的边长为4,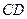 是
是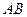 边上的高,
边上的高,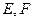 分别是
分别是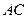 和
和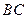 边的中点,现将△
边的中点,现将△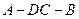 .
.
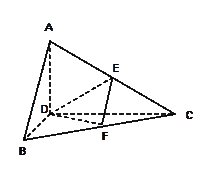
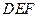 的位置关系,并说明理由;
的位置关系,并说明理由;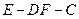 的余弦值;
的余弦值;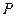 ,使
,使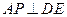 ?证明你的结论.
?证明你的结论.