题目内容
【题目】为了解学生身高情况，某校以 
的比例对全校1000名学生按性别进行分层抽样调查，已知男女比例为 
，测得男生身高情况的频率分布直方图（如图所示）：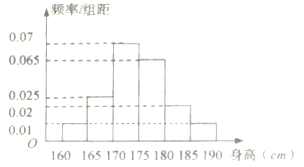
（1）计算所抽取的男生人数，并估计男生身高的中位数（保留两位小数）；
（2）从样本中身高在 
之间的男生中任选2人，求至少有1人身高在 
之间的概率．
【答案】
（1）解：由题意得，所抽取的男生人数为：
1000×8%× 
=40人
依据样本频率分布直方图：0.01×5+0.025×5+x=0.5 得x=0.325 ，而身高170~175之间的频率为0.35，所以中位数为170+5× 
≈174.64cm
（2）解：样本中身高在180～185 cm之间的男生有4人，设其编号为①，②，③，④，样本中身高在185～190 cm之间的男生有2人，设其编号为⑤，⑥，从上述6人中任取2人的共有：
（①，②）（①，③）（①，④）（①，⑤）（①，⑥）
（②，③）（②，④）（②，⑤）（②，⑥）
（③，④）（③，⑤）（③，⑥）
（④，⑤）（④，⑥）
（⑤，⑥）
故从样本中身高在180～190 cm之间的男生中任选2人的所有可能结果数为15，至少有1人身高在185～190 cm之间的可能结果数为9，因此，所求概率P2＝ 
＝ 
【解析】(1)由频率分布直方图能求出所抽男生的人数和中位数。(2)样本中身高在180～185 cm之间的男生有4人，设为①，②，③，④样本中身高在185～190 cm之间的男生有2人，设为⑤，⑥利用列举法能求出至少有1人身高在185～190 cm之间的概率。
【考点精析】关于本题考查的频率分布直方图和用样本的频率分布估计总体分布，需要了解频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚的看到整个样本数据的频率分布情况，并由此估计总体的分布情况才能得出正确答案．
名校课堂系列答案
