Question

【题目】已知向量 ，记函数 .求：
（I）函数 的最小值及取得最小值时 的集合；
（II）求函数f(x) 的单调增区间。

Answer 1

【答案】解：由题意： ，

所以，

因此，

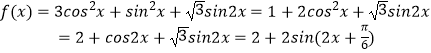
当 ，即 时, 取得最小值.

此时 ， 最小值=

（II）函数 的单调递增区间.

解：由题意：

即

于是, 的单调递增区间是

【解析】(1)故解集平面向量的坐标运算整理原式，再结合二倍角的余弦公式以及辅助角公式得到正弦型函数，利用正弦型函数的最值情况得出当f(x) 取得最小值和最大值时x的集合。(2)根据(1)的化简结果利用正弦型函数的单调性整体思想代入求出x的取值范围，再将其变成区间的形式。
【考点精析】关于本题考查的二倍角的余弦公式和正弦函数的单调性，需要了解二倍角的余弦公式：；正弦函数的单调性：在上是增函数；在上是减函数才能得出正确答案．