题目内容
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点. 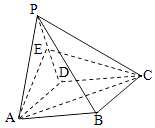
(1)求证:PB⊥AC.
(2)求二面角E﹣AC﹣D的正切值.
【答案】
(1)证明:设AD中点为F连接BF、PF.
∵PA=PD=AB=a,∴ ![]() ,
,
∴ ![]() .
.
∴△ABC∽△FAB,∴AC⊥BF,
又∵PF⊥AD,又∵平面PAD⊥平面ABCD.
平面PAD∩平面ABCD=AD,
∴PF⊥面ABC,∴PF⊥AC,
∴AC⊥平面PBF,AC⊥PB.
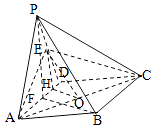
(2)解:(2)过E作EH∥PF,EH交AD于H,
过H作HO⊥AC,交AC于O,连接EO.
由(1)知EH⊥面ACD,HO⊥AC,
∴∠EOH为二面角E﹣AC﹣D的平面角
![]() .
.
![]() .
.
∴ ![]() .
.
∴二面角E﹣AC﹣D的正切值为 ![]() .
.
【解析】(1)设AD中点为F,连接BF、PF,推导出△ABC∽△FAB,从而AC⊥BF,推导出PF⊥AC,由此能证明AC⊥PB.(2)过E作EH∥PF,EH交AD于H,过H作HO⊥AC,交AC于O,连接EO,则∠EOH为二面角E﹣AC﹣D的平面角,由此能求出二面角E﹣AC﹣D的正切值.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目