��Ŀ����
����Ŀ��ij��˾�����һ���Ȼ���״�Ļ�̳����ͼ��ʾ��,���Ȼ������Ե�![]() ΪԲ�ĵ�����ͬ��Բ�����ӳ���ͨ����
ΪԲ�ĵ�����ͬ��Բ�����ӳ���ͨ����![]() ,
,![]() �������߶�Χ�ɣ���Բ��
�������߶�Χ�ɣ���Բ��![]() ��Բ��
��Բ��![]() ����Բ�İ뾶�ֱ�Ϊ
����Բ�İ뾶�ֱ�Ϊ![]() ��,Բ�Ľ�Ϊ�������ȣ���
��,Բ�Ľ�Ϊ�������ȣ���

(1)��![]() ,
,![]() ,��̳�������
,��̳�������
(2)���ʱ��Ҫ���ǻ�̳��Ե��ʵ�߲��֣���װ������,��ֱ֪�߲��ֵ�װ�η���Ϊ60Ԫ/��,���߲��ֵ�װ�η���Ϊ90Ԫ/��,Ԥ������ܼ�1200Ԫ,���߶�AD�ij���Ϊ����ʱ,��̳��������
���𰸡���1��![]() ����2�����߶�
����2�����߶�![]() �ij�Ϊ5��ʱ����̳��������.
�ij�Ϊ5��ʱ����̳��������.
��������
(1)�������ε������ʽ,��������������֮���������̳��������ɣ�
(2)���û�����ʽ����Ԥ������ܼ�1200Ԫ�ɵõ���ʽ,�������̳������ı���ʽ,��ϵõ��ĵ�ʽ,ͨ���䷽���������������ʱ, �߶�AD�ij���.
(1)�軨̳�����ΪSƽ����.
![]()
![]()
![]()
�𣺻�̳�����Ϊ![]() ��
��
(2) Բ��![]() �ij�Ϊ
�ij�Ϊ![]() �ף�Բ��
�ף�Բ��![]() �ij�Ϊ
�ij�Ϊ![]() �ף��߶�
�ף��߶�![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
������֪![]() ��
��
��![]() * ��
* ��
![]() ��
��
��*ʽ֪��![]() ��
��
��![]() ��
��![]()
����![]() =
=![]()
��![]() ʱ��
ʱ��![]() ȡ�����ֵ����
ȡ�����ֵ����![]() ʱ����̳��������
ʱ����̳��������
�𣺵��߶�![]() �ij�Ϊ5��ʱ����̳��������.
�ij�Ϊ5��ʱ����̳��������.

 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�����Ŀ��Ϊ������ȫ����ѧ�����ʽ���������ۻ��ƣ�����ѧ�������μ����������������ӡ��������ѧ�����ʽ�������2014����������Ҫ���ѧУÿѧ�ڿ�չ���DZ�У���꼶ѧ���ġ��������Թ�����������ѧ��ÿ��ѧ���ܷ������ȼ�.ijУ������Ը���ѧ����ÿѧ�ڽ���һ�����ʽ������ԣ�������С��ͬѧ����ѧ�����ʽ������Ե��ܷ����.
ѧ�� | 1 | 2 | 3 | 4 | 5 | 6 |
�ܷ� | 512 | 518 | 523 | 528 | 534 | 535 |
��1��������ϱ��ṩ�����ݣ������ϵ��![]() ˵��
˵��![]() ��
��![]() ��������س̶ȣ�������С���˷����
��������س̶ȣ�������С���˷����![]() ����
����![]() �����Իع鷽�̣��������ϵ��������λС������
�����Իع鷽�̣��������ϵ��������λС������
��2����������ѧ��������ѧУ���� ������������540������Ϊ����ȼ�����֪С�����ڵ�ѧϰС��10��ͬѧ��6��������Ϊ���㣬���Ժ�ͬѧ�Ƕ�֪�����Լ����ֵܷ���֪�����˵��ܷ֣�С������ĸ�С����4��ͬѧ��绰ѯ�ʶԷ��ɼ��������ͬѧ��![]() �ˣ���
�ˣ���![]() �ķֲ��к�����.
�ķֲ��к�����.
�ο���ʽ�� 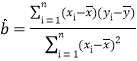 ��
��![]() ��
��
���ϵ��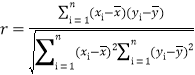 ��
��
�ο����ݣ�![]() ��
��![]() .
.
����Ŀ��ijУ���п���ʵ�飬�Ұ�Ϊʵ��࣬�װ�Ϊ�ԱȰ࣬�����������50�ˣ�һ����������в��ԣ��ɼ����±�
�װ�ɼ� |
|
|
|
|
|
���� | 4 | 20 | 15 | 10 | 1 |
�Ұ�ɼ� |
|
|
|
|
|
���� | 1 | 11 | 23 | 13 | 2 |
��1���ִӼװ�ɼ�λ��![]() �ڵ��Ծ��г�ȡ9�ݽ����Ծ�������������ʲô������������������д�����ij������
�ڵ��Ծ��г�ȡ9�ݽ����Ծ�������������ʲô������������������д�����ij������
��2���������![]() �����������ж��ж�������Ϊ������������β����гɼ��IJ�����ʵʩ����ʵ���йء�
�����������ж��ж�������Ϊ������������β����гɼ��IJ�����ʵʩ����ʵ���йء�
�ɼ�С��100 | �ɼ���С��100 | �ϼ� | |
�װ� | 50 | ||
�Ұ� | 50 | ||
�ϼ� | 36 | 64 | 100 |


