题目内容

已知△ABC中，B（-2，0），C（2，0），△ABC的周长为12，动点A的轨迹为曲线E．
（1）求曲线E的方程；
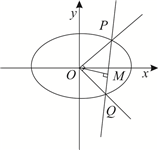
（2）设P、Q为E上两点，
OP
•
OQ
=0，过原点O作直线PQ的垂线，垂足为M，证明|OM|为定值．
（1）∵|AB|+|AC|+|BC|=12，|BC|=4，
∴|AB|+|AC|=8＞4，
∴A的轨迹为椭圆，且2a=8，2c=4，
∴a2=16，c2=4，b2=12，
∵A，B，C不能共线，∴A点不能在x轴上，
∴曲线E的方程为
x2
16
+
y2
12
=1(y≠0)…（5分）
（2）证明：设直线PQ的方程为x=ny+m，
由
x=ny+m
x2
16
+
y2
12
=1
得（4n2+3）y2+8mny+4m2-48=0，
∴y1+y2=-
8mn
4n2+3
，y1•y2=
4m2-48
4n2+3
…（2分）
∴x1x2=(ny1+m)(ny2+m)=n2y1y2+mn(y1+y2)+m2=
3m2-48n2
4n2+3
…（1分）
∵
OP
•
OQ
=0，∴x1x2+y1•y2=0，
∴
3m2-48n2
4n2+3
+
4m2-48
4n2+3
=0，
∴7m2-48n2-48=0…（1分）
∵|OM|为点O（0，0）到直线PQ：x-ny-m=0的距离，
∴|OM|=
|-m|
n2+1
，
∴|OM|2=
m2
n2+1
…（1分）
由7m2-48n2-48=0得m2=
48
7
(n2+1)…（1分）
∴|OM|2=
48
7
(n2+1)
n2+1
=
48
7
，
∴|OM|为定值…（1分）
练习册系列答案
相关题目
如图，以
3
2
为离心率的椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右顶点分别为A和B，点P是椭圆位于x轴上方的一点，且△PAB的面积最大值为2．
（Ⅰ）求椭圆方程；
（Ⅱ）设点Q是椭圆位于x轴下方的一点，直线AP、BQ的斜率分别为k1，k2，若k1=7k2，设△BPQ与△APQ的面积分别为S1，S2，求S1-S2的最大值．
已知椭圆C的焦点在x轴上，O为坐标原点，F是一个焦点，A是一个顶点．若椭圆的长轴长是6，且cos∠OFA=
2
3
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求点R（0，1）与椭圆C上的点N之间的最大距离；
（Ⅲ）设Q是椭圆C上的一点，过Q的直线l交x轴于点P（-3，0），交y轴于点M．若
MQ
=2
QP
，求直线l的斜率．
已知抛物线C的顶点为O（0，0），焦点F（0，1）
（Ⅰ）求抛物线C的方程；
（Ⅱ）过F作直线交抛物线于A、B两点．若直线OA、OB分别交直线l：y=x-2于M、N两点，求|MN|的最小值．
如图，已知焦点在x轴上的椭圆
x2
20
+
y2
b2
=1(b＞0)经过点M（4，1），直线l：y=x+m交椭圆于A，B两不同的点．
（1）求该椭圆的标准方程；
（2）求实数m的取值范围；
（3）是否存在实数m，使△ABM为直角三角形，若存在，求出m的值，若不存，请说明理由．
已知O为坐标原点，F是抛物线E：y2=4x的焦点．
（Ⅰ）过F作直线l交抛物线E于P，Q两点，求
OP
•
OQ
的值；
（Ⅱ）过点T（t，0）作两条互相垂直的直线分别交抛物线E于A，B，C，D四点，且M，N分别为线段AB，CD的中点，求△TMN的面积最小值．
已知抛物线C的方程为x2=4y，直线y=2与抛物线C相交于M，N两点，点A，B在抛物线C上．
（Ⅰ）若∠BMN=∠AMN，求证：直线AB的斜率为
2
；
（Ⅱ）若直线AB的斜率为
2
，求证点N到直线MA，MB的距离相等．
如图，椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率e=
5
5
，过F1的直线交椭圆于M、N两点，且△MNF2周长为4
5
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）已知过椭圆中心，且斜率为k（k≠0）的直线与椭圆交于A、B两点，P是线段AB的垂直平分线与椭圆E的一个交点，若△APB的面积为
40
9
，求k的值．
已知抛物线C1：y2=8x与双曲线C2：
x2
a2
-
y2
b2
=1（a＞0，b＞0）有公共焦点F2，点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（1）求双曲线C2的方程；
（2）以双曲线C2的另一焦点F1为圆心的圆M与直线y=
3
x相切，圆N：（x-2）2+y2=1．过点P（1，
3
）作互相垂直且分别与圆M、圆N相交的直线l1和l2，设l1被圆M截得的弦长为s，l2被圆N截得的弦长为t，问：
s
t
是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网